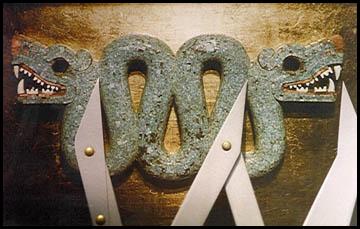Golden Ratio
GOLDEN RATIO
DEFINITION
It is said that two quantities are in a golden ratio also known under names golden section, golden mean [1], medial section, golden cut [2], extreme and mean ratio [3] when the following, expressed in algebraic form, is true:
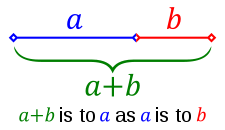
In other words if the whole is to the larger as the larger is to the smaller. The golden ratio is irrational mathematical constant. Its value is 1.6180339887... The golden ratio is symbolised by the Greek letter 
(phi) and also by the less known τ (tau).
This mathematical proportion is often recognized as 'aesthetically pleasing'. Because of that golden ratio found its use in many different fields like mathematics, architecture, geometry, science, biology, nature, art and design.
The actual discovery of the golden ratio can be lead back to the ancient Greeks and the Pythagoras. The greek mathematician Euclid of Alexandria (365BC - 300BC) mentioned the golden mean.
CALCULATION
Method for calculation of golden ratio constant is beginning from the following algebraic formula:
From the formula we obtain that a is equal b/, so we can replace all occurences of a:
Devided by b formula changes to:
Now we need to multiply formula by and by moving content of the right side to the left side we get quadratic equation:
The only positive result to above equation is the irrational number we have already presented:
GEOMETRY AND MATHEMATICS
Fibonacci introduced to us, the Fibonacci-Numbers:
1,2,3,5,8,13,21,34,55,89,144,233,377,....
Every number of this alignment equals to 0,168 if you divide it with the one before it, and 1,618 when you divide it with the number after it. These are the relationships between the larger and smaller numbers in the golden ratio. Below you can see example for division of bigger by smaller number:
and by smaller devided by bigger number:
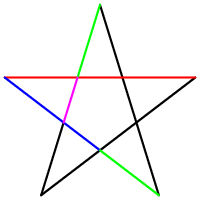
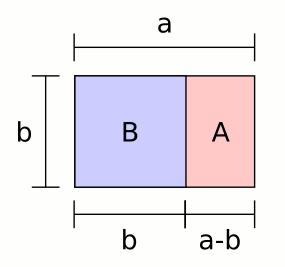
There are many shapes in which golden ratio were discovered. Examples of those you can see on the right side.
| Pentagram | Golden rectangle |
|---|---|
|
|
|
| Image Illustrates the hidden golden ratio in the very special shape, pentagram. | A rectangle is a golden rectangle when the sides are in the 1:0,618 proportion. |
ART & DESIGN
Since the beginning of ART & Design, the artist and designers used the golden ratio in order to manage and achieve beauty and balance in their creations. In the following table you can see few examples for all.
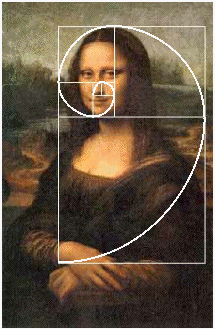
| Mona-Liza | Aztek decorations | Credit cards |
|---|---|---|
|
|
|
|
| In Mona-Liza painting you can find many golden rectangles that together create golden spiral. | The space between the two heads is exacly Phi times the width of the heads.[Brooker] | if you measure a credit-card, the outcome would be a perfect golden rectangle.[Batterywholesaler] |
Architecture
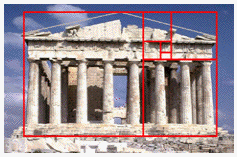
There is many examples of golden ratio even in architecture. Architect were inspired by this "sacred ratio" already in times of Pyramids. Even in Greek you can find golden rectangles, spirals, etc. In the table below you can find several examples.
| Great Pyramid of Giza | Parthenon | Engineering Plaza |
|---|---|---|
|
|
|
|
| The Great Pyramid has proportions designed according to golden ratio. | Even in proportions of Parthenon you can find golden spiral consisting of golden rectangles. | The Designers of this new Plaza have chosen the Fibonacci series spiral, or also called the golden mean to design this new state of the art plaza.[Dr Knott, 1996-2005] |
Related Links
REFERENCES
[Wikipedia, Golden Ratio, 2005] Wikipedia.org, Golden Ratio, 19.10.2005, http://en.wikipedia.org/wiki/Golden_ratio
[Absoluteastronomy] Absoluteastronomy, Golden Ratio, http://www.absoluteastronomy.com/encyclopedia/g/go/golden_ratio.htm
[Kaphammel, 2000] Günther Kahammel, Der goldene Schnitt, 1. Auflage, Braunschweig, 2000
[Wikipedia, Golden rectangle, 2005] Wikipedia.org, Golden rectangle, 24.10.2005, http://en.wikipedia.org/wiki/Golden_rectangle
[Wikipedia, Pentagram, 2005] Wikipedia.org, Pentagram, 29.10.2005, http://en.wikipedia.org/wiki/Pentagram
[Brooker] Carolyn Brooker, The Golden Ratio in the Arts, University of Bath, http://students.bath.ac.uk/ma1caab/art.html
[Dr Knott, 1996-2005] Dr Ron Knott, Fibonacci Numbers and The Golden Section in Art, Architecture and Music, University of Surrey, 1996-2005, http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibInArt.html
[Batterywholesaler] Batterywholesaler, Credit Cards, http://www.batterywholesaler.co.uk/battery_images
[Obara] Samuel Obara, Golden Ratio in Art and Architecture, University of Georgia, http://jwilson.coe.uga.edu/EMT668/EMAT6680.2000/Obara/Emat6690/Golden%20Ratio/golden.html
[Livio, 2002] Mario Livio, The golden ratio and aesthetics, November 2002, http://plus.maths.org/issue22/features/golden/
- ↑ Template:Cite book
- ↑ Summerson John, Heavenly Mansions: And Other Essays on Architecture (New York: W.W. Norton, 1963) p. 37. "And the same applies in architecture, to the rectangles representing these and other ratios (e.g. the 'golden cut'). The sole value of these ratios is that they are intellectually fruitful and suggest the rhythms of modular design."
- ↑ Euclid, Elements, Book 6, Definition 3.