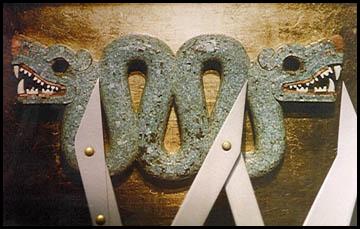Golden Ratio: Difference between revisions
| Line 92: | Line 92: | ||
<center> | |||
The evidence of the golden ratio was proved on many different creations, like the Aztek decorations below: | The evidence of the golden ratio was proved on many different creations, like the Aztek decorations below: | ||
| Line 98: | Line 98: | ||
The space between the two heads is exacly Phi times the width of the heads. [4] | The space between the two heads is exacly Phi times the width of the heads. [4] | ||
</center> | |||
Revision as of 21:56, 25 October 2005
GOLDEN RATIO
DEFINITION
- In the Mathmatics the number 1.61803399 is the golden ratio. [1]
- Two quantities are said to be in the golden ratio, if "the whole is to the larger as the larger is to the smaller" [2]
INTRODUCTION
The use of the golden ratio can be found in many different fields. In mathematics, architecture, geometry, science, biology, nature, art, design and many others.
Other names of this word are as follows: the golden mean, golden section, golden number, divine proportion or sectio divina(golden Cut).
HISTORY
The Golden ratio can be found as far back to the building of the Great Pyramid of Giza around 2560 BC.
The actual discovery of the golden ratio can be lead back to the ancient Greeks and the Pythagoras. The greek mathematician Euclid of Alexandria (365BC - 300BC) mentioned the golden mean.
Even Plato, the Greek Philosopher was occupied by the Golden ratio.
GOLDEN RATIO IN GEOMETRY AND MATHEMATICS
Fibonacci introduced to us, the Fibonacci-Numbers:
1,2,3,5,8,13,21,34,55,89,144,233,377,....
Every number of this alignement equals to 0,168 if you divide it with the one before it, and 1,618 when you divide it with the number after it.
These are the relationships between the larger and smaller numbers in the golden ratio.
Below you can find an example of the Fibonacci-Numbers
The Golden Ratio can also be found in different kinds of shapes. This goes on from the usual rechangle, through different kinds of triangles and to the very complicated shapes like the pentacle.
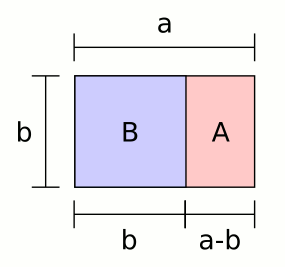
A rectanle is a Golden rectangle when the sides are in the 1:0,618 proportion. Below is an example of this kind of shape.
Image 1: Golden Rectangle [8]
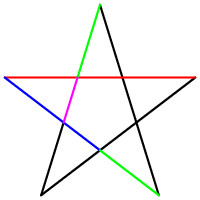
Another shape where the golden ratio can be found is the Pentagramm. This image below, illustrates the hidden golden ratio in this very special shape.
Image 2: Golden Pentagramm [9]
GOLDEN RATIO IN ART & DESIGN
Since the beginning of ART & Design, the artist and designers used the golden ratio in order to manage and achieve beauty and balance in their creations.
The evidence of the golden ratio was proved on many different creations, like the Aztek decorations below:
The space between the two heads is exacly Phi times the width of the heads. [4]
The California Polytechnic State University is planing to build a new Engineering Plaza. This new construction is based on the Fibonacci numbers. The whole plan also bases on some shapes, which can be used to show the meaning of the golden ratio. The Designers of this new Plaza have chosen the Fibonacci series spiral, or also called the golden mean to design this new state of the art plaza. Below you can see, what the plaza should look like:
California Polytechnic Engineering Plaza [5]
Even the mountainbike shown below, has the golden ratio built in. Take a look at the image, and the marked golden sections of the bike.
Mountainbike Trek Fuel 90 (belongs to Brian Agron of Fairfax)[5]
So the use of the golden ratio can not only be found in ancient paintings and sculptures, but also in the stunning creations still to come.
Did you know, that if you measure a credit-card, the outcome would be a perfect golden rectangle. This ofcourse shows, that the golden ratio is very well in use. Even if it comes to the proportions and masses of everyday things like credit cards.
Credit Cards [6]
References
[1]. Wikipedia.org: Golden Ratio
[2]. Golden Ratio:
[3]. University of Georgia: Golden Ratio in Art and Architecture; Samuel Obara
[4]. THE GOLDEN RATIO IN THE ARTS
[5]. Fibonacci Numbers and The Golden Section in Art, Architecture and Music
[6]. Credit Cards
[7]. Online Article: The golden ratio and aesthetics; by Mario Livio; November 2002
[8]. Wikipedia.org: Golden Rectangle
[9]. Wikipedia.org: Pentagramm
Back to Gruppe 09