Golden Ratio: Difference between revisions
| Line 8: | Line 8: | ||
* In the Mathmatics the number 1.61803399 is the golden ratio. [1] | * In the Mathmatics the number 1.61803399 is the golden ratio. [1] | ||
* The golden ratio is sybolised by the Greek letter [[Image:phi.jpg]] ([phi]) and also by the less know τ ([tau]) | * The golden ratio is sybolised by the Greek letter [[Image:phi.jpg]] ([[phi]]) and also by the less know τ ([tau]) | ||
===Introduction=== | ===Introduction=== | ||
Revision as of 15:56, 25 October 2005
Golden Ratio
Definition
- In the Mathmatics the number 1.61803399 is the golden ratio. [1]
- The golden ratio is sybolised by the Greek letter File:Phi.jpg (phi) and also by the less know τ ([tau])
Introduction
The use of the golden ratio can be found in many different fields. In mathematics, architecture, geometry, science, biology, nature, art, design and many others.
Other names of this word are as follows: the golden mean, golden section, golden number, divine proportion or sectio divina(golden Cut).
History
The golden ratio can be found, as far back to the studies of the ancient egyptians. They might have used and understood this Study, But the actual discovery of the golden ratio can be lead back to the ancient Greeks and the Pythagoras. The greek mathematician Euclid of Alexandria mentioned the golden mean.
Golden ratio in geometry & mathematics
Not only is the golden ratio a value in the mathematics...
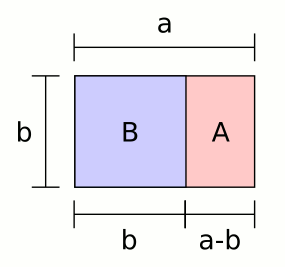
Furthermore, the Golden Ratio can be found in different kinds of shapes. This goes on from the usual rechangle, through different kinds of triangles and to the very complicated shapes like the pentacle.
A rectanle is a Golden rectangle when the sides are in the 1:0,618 proportion. Below is an example of this kind of shape.
Image 1: Golden Rectangle
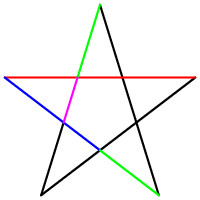
Another shape where the golden ratio can be found is the Pentagramm. This image below, illustrates the hidden golden ratio in this very special shape.
Image 2: Golden Pentagramm
Golden ratio in art & design
Conclusion
Resources
[1]. Wikipedia.org: Golden Ratio http://en.wikipedia.org/wiki/Golden_ratio
[2]. Desktop Publishing: http://desktoppub.about.com/od/goldenrectangle/
[3].
Back to Gruppe 09