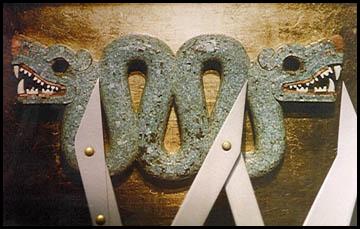Golden Ratio: Difference between revisions
No edit summary |
No edit summary |
||
| Line 5: | Line 5: | ||
---- | ---- | ||
===DEFINITION=== | ===DEFINITION=== | ||
It is said that two quantities are in a golden ratio also known under names '''golden section''', '''golden mean''' <ref name="livio">{{cite book|last=Livio|first=Mario|year=2002|title=The Golden Ratio: The Story of Phi, The World's Most Astonishing Number|publisher=Broadway Books|location=New York|isbn=0-7679-0815-5}}</ref>, '''medial section''', '''golden cut''' <ref>Summerson John, ''Heavenly Mansions: And Other Essays on Architecture'' (New York: W.W. Norton, 1963) p. 37. "And the same applies in architecture, to the [[rectangle]]s representing these and other ratios (e.g. the 'golden cut'). The sole value of these ratios is that they are intellectually fruitful and suggest the rhythms of modular design."</ref>, '''extreme and mean ratio''' <ref name="Elements 6.3">Euclid, ''[http://aleph0.clarku.edu/~djoyce/java/elements/toc.html Elements]'', Book 6, Definition 3.</ref> when the following, expressed in algebraic form, is true: | |||
:<math> \frac{a+b}{a} = \frac{a}{b} = \varphi\,.</math> | |||
{{Quotation|Two quantities are said to be in the golden ratio, if "the whole is to the larger as the larger is to the smaller" |[Absoluteastronomy]}} | {{Quotation|Two quantities are said to be in the golden ratio, if "the whole is to the larger as the larger is to the smaller" |[Absoluteastronomy]}} | ||
| Line 32: | Line 35: | ||
The actual discovery of the golden ratio can be lead back to the ancient Greeks and the Pythagoras. The greek mathematician Euclid of Alexandria (365BC - 300BC) mentioned the golden mean. | The actual discovery of the golden ratio can be lead back to the ancient Greeks and the Pythagoras. The greek mathematician Euclid of Alexandria (365BC - 300BC) mentioned the golden mean. | ||
{{Quotation|A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.| Euclid of Alexandria(ca. 300BC)}} | |||
{{Quotation| | |||
Even Plato, the Greek Philosopher was occupied by the Golden ratio. | Even Plato, the Greek Philosopher was occupied by the Golden ratio. | ||
Revision as of 18:10, 5 November 2009
GOLDEN RATIO
DEFINITION
It is said that two quantities are in a golden ratio also known under names golden section, golden mean [1], medial section, golden cut [2], extreme and mean ratio [3] when the following, expressed in algebraic form, is true:
- <math> \frac{a+b}{a} = \frac{a}{b} = \varphi\,.</math>
The golden ratio is symbolised by the Greek letter 
(phi) and also by the less known τ (tau).
INTRODUCTION
The use of the golden ratio can be found in many different fields. In mathematics, architecture, geometry, science, biology, nature, art, design and many others.
Other names of this word are as follows: the golden mean, golden section, golden number, divine proportion or sectio divina(golden Cut).
HISTORY
The Golden ratio can be found as far back to the building of the Great Pyramid of Giza around 2560 BC.
The actual discovery of the golden ratio can be lead back to the ancient Greeks and the Pythagoras. The greek mathematician Euclid of Alexandria (365BC - 300BC) mentioned the golden mean.
Even Plato, the Greek Philosopher was occupied by the Golden ratio.
GOLDEN RATIO IN GEOMETRY AND MATHEMATICS
Fibonacci introduced to us, the Fibonacci-Numbers:
1,2,3,5,8,13,21,34,55,89,144,233,377,....
Every number of this alignement equals to 0,168 if you divide it with the one before it, and 1,618 when you divide it with the number after it.
These are the relationships between the larger and smaller numbers in the golden ratio.
Below you can find an example of the Fibonacci-Numbers
[Kaphammel, 2000]
The Golden Ratio can also be found in different kinds of shapes. This goes on from the usual rechangle, through different kinds of triangles and to the very complicated shapes like the pentacle.
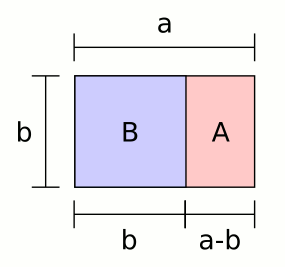
A rectanle is a Golden rectangle when the sides are in the 1:0,618 proportion. Below is an example of this kind of shape.
[Wikipedia, Golden rectangle, 2005]
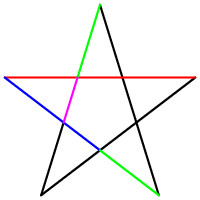
Another shape where the golden ratio can be found is the Pentagramm. This image below, illustrates the hidden golden ratio in this very special shape.
[Wikipedia, Pentagram, 2005]
GOLDEN RATIO IN ART & DESIGN
Since the beginning of ART & Design, the artist and designers used the golden ratio in order to manage and achieve beauty and balance in their creations.
The evidence of the golden ratio was proved on many different creations, like the Aztek decorations below:
[Brooker]
The space between the two heads is exacly Phi times the width of the heads.
The California Polytechnic State University is planing to build a new Engineering Plaza. This new construction is based on the Fibonacci numbers. The whole plan also bases on some shapes, which can be used to show the meaning of the golden ratio. The Designers of this new Plaza have chosen the Fibonacci series spiral, or also called the golden mean to design this new state of the art plaza. Below you can see, what the plaza should look like.
[Dr Knott, 1996-2005]
Even the mountainbike shown below, has the golden ratio built in. Take a look at the image, and the marked golden sections of the bike.
[Dr Knott, 1996-2005]
Mountainbike Trek Fuel 90 (belongs to Brian Agron of Fairfax)
So the use of the golden ratio can not only be found in ancient paintings and sculptures, but also in the stunning creations still to come.
|
Did you know, that if you measure a credit-card, the outcome would be a perfect golden rectangle. This ofcourse shows, that the golden ratio is very well in use. Even if it comes to the proportions and masses of everyday things like credit cards. [Batterywholesaler] |
CONCLUSION
The very simple and suitable conclusion is that the Golden Ratio can be found everywhere. In probably any field you can think of. And in many, not all, but at least very many cases, the Golden Ratio is used to improve something. Some don't even know, that something they have created respects the laws of the Golden Ratio. This is kind of like the ancient egyptians, who probably used the Golden Ratio, but never thought of, and so never really discovered it.
So look for it, maybe you can discover an ancient theory in something quite modern...
Related Links
REFERENCES
[Wikipedia, Golden Ratio, 2005] Wikipedia.org, Golden Ratio, 19.10.2005, http://en.wikipedia.org/wiki/Golden_ratio
[Absoluteastronomy] Absoluteastronomy, Golden Ratio, http://www.absoluteastronomy.com/encyclopedia/g/go/golden_ratio.htm
[Kaphammel, 2000] Günther Kahammel, Der goldene Schnitt, 1. Auflage, Braunschweig, 2000
[Wikipedia, Golden rectangle, 2005] Wikipedia.org, Golden rectangle, 24.10.2005, http://en.wikipedia.org/wiki/Golden_rectangle
[Wikipedia, Pentagram, 2005] Wikipedia.org, Pentagram, 29.10.2005, http://en.wikipedia.org/wiki/Pentagram
[Brooker] Carolyn Brooker, The Golden Ratio in the Arts, University of Bath, http://students.bath.ac.uk/ma1caab/art.html
[Dr Knott, 1996-2005] Dr Ron Knott, Fibonacci Numbers and The Golden Section in Art, Architecture and Music, University of Surrey, 1996-2005, http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibInArt.html
[Batterywholesaler] Batterywholesaler, Credit Cards, http://www.batterywholesaler.co.uk/battery_images
[Obara] Samuel Obara, Golden Ratio in Art and Architecture, University of Georgia, http://jwilson.coe.uga.edu/EMT668/EMAT6680.2000/Obara/Emat6690/Golden%20Ratio/golden.html
[Livio, 2002] Mario Livio, The golden ratio and aesthetics, November 2002, http://plus.maths.org/issue22/features/golden/
- ↑ Template:Cite book
- ↑ Summerson John, Heavenly Mansions: And Other Essays on Architecture (New York: W.W. Norton, 1963) p. 37. "And the same applies in architecture, to the rectangles representing these and other ratios (e.g. the 'golden cut'). The sole value of these ratios is that they are intellectually fruitful and suggest the rhythms of modular design."
- ↑ Euclid, Elements, Book 6, Definition 3.