Hyperbolic trees: Difference between revisions
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
== Short Description == | == Short Description == | ||
{{Quotation|...The essence of this scheme is to lay out the hierarchy in a uniform way on a hyperbolic plane and map this plane onto a circular display region. This supports a smooth blending between focus and context, as well as continuous redirection of the focus...| [John Lamping et al., 1995]}} | {{Quotation|[...]The essence of this scheme is to lay out the hierarchy in a uniform way on a hyperbolic plane and map this plane onto a circular display region. This supports a smooth blending between focus and context, as well as continuous redirection of the focus[...] Two salient properties of the figures are: First that components diminish in size as they move outwards, and second that there is an exponential growth in the number of components. These properties - "fisheye" distortion and the ability to uniformly embed an exponentially growing structure - are the aspects of this construction. [...]| [John Lamping et al., 1995]}} | ||
== Suitable Datatypes == | == Suitable Datatypes == | ||
Revision as of 18:49, 27 April 2006
Authors
Short Description
Suitable Datatypes
This visualization method can be used on hierarchies. With its characteristics the method is especially suitable for the visualization and manipulation of large hierachical data.
Figures
The Circle Limit IV 1960 woodcut in black and ocre, printed from 2 blocks by Maurits Cornelis Escher (1898-1972) was the original inspiration for the hyperbolic browser.
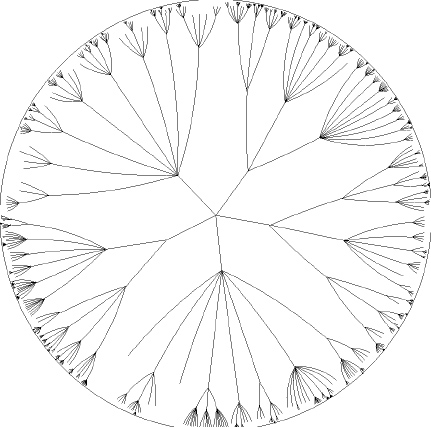
The following figure shows an original hyperbolic tree with its origin in the center and 1004 nodes:
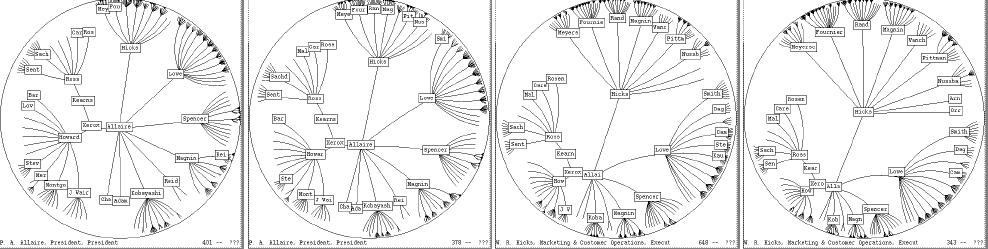
The origin does not have to be in the center of the fisheye. The focus can be changed by the user either by clicking on any visible point to bring it into focus at the center or by dragging any visble point interactively to any other position:
Examples and use cases
Evaluation
References
[Lamping, et al., 1995] John Lamping, Ramana Rao, Peter Pirolli, A Focus+Context Technique Based on Hyperbolic Geometry for Visualizing Large Hierarchies, Xerox Palo Alto Research Center, Last Retrieved at: April 27, 2006. http://www.acm.org/sigchi/chi95/Electronic/documnts/papers/jl_bdy.htm
[edit] 3 References