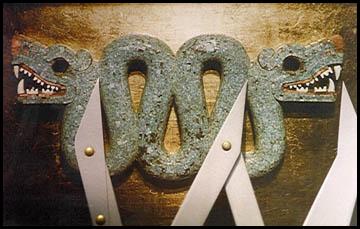Golden Ratio: Difference between revisions
| Line 29: | Line 29: | ||
===Golden ratio in geometry & mathematics=== | ===Golden ratio in geometry & mathematics=== | ||
Fibonacci introduced to us, the Fibonacci-Numbers: | Fibonacci introduced to us, the Fibonacci-Numbers: | ||
1,2,3,5,8,13,21,34,55,89,144,233,377,.... | 1,2,3,5,8,13,21,34,55,89,144,233,377,.... | ||
Every number of this alignement equals to 0,168 if you divide it with the one before it, and 1,618 when you divide it with the number after it. | Every number of this alignement equals to 0,168 if you divide it with the one before it, and 1,618 when you divide it with the number after it. | ||
These are the relationships between the larger and smaller numbers in the golden ratio. | These are the relationships between the larger and smaller numbers in the golden ratio. | ||
Below you can find an example of the Fibonacci-Numbers | Below you can find an example of the Fibonacci-Numbers | ||
Revision as of 17:40, 25 October 2005
Golden Ratio
Definition
- In the Mathmatics the number 1.61803399 is the golden ratio. [1]
- The golden ratio is sybolised by the Greek letter
(phi) and also by the less know τ (tau).
Introduction
The use of the golden ratio can be found in many different fields. In mathematics, architecture, geometry, science, biology, nature, art, design and many others.
Other names of this word are as follows: the golden mean, golden section, golden number, divine proportion or sectio divina(golden Cut).
History
The Golden ratio can be found as far back to the building of the Great Pyramid of Giza around 2560 BC.
The actual discovery of the golden ratio can be lead back to the ancient Greeks and the Pythagoras. The greek mathematician Euclid of Alexandria (365BC - 300BC) mentioned the golden mean.
Even Plato, the Greek Philosopher was occupied by the Golden ratio.
Golden ratio in geometry & mathematics
Fibonacci introduced to us, the Fibonacci-Numbers:
1,2,3,5,8,13,21,34,55,89,144,233,377,....
Every number of this alignement equals to 0,168 if you divide it with the one before it, and 1,618 when you divide it with the number after it.
These are the relationships between the larger and smaller numbers in the golden ratio.
Below you can find an example of the Fibonacci-Numbers
The Golden Ratio can be found in different kinds of shapes. This goes on from the usual rechangle, through different kinds of triangles and to the very complicated shapes like the pentacle.
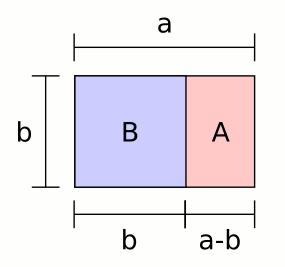
A rectanle is a Golden rectangle when the sides are in the 1:0,618 proportion. Below is an example of this kind of shape.
Image 1: Golden Rectangle
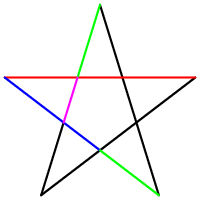
Another shape where the golden ratio can be found is the Pentagramm. This image below, illustrates the hidden golden ratio in this very special shape.
Image 2: Golden Pentagramm
Golden ratio in ART & DESIGN
Since the beginning of ART & Design, the artist and designers used the golden ratio in order to manage and achieve beauty and balance in their creations.
The evidence of the golden ratio was proved on many different creations, like the Aztek decorations below:
The space between the two heads is exacly Phi times the width of the heads.
Resources
[1]. Wikipedia.org: Golden Ratio
[2]. University of Georgia: Golden Ratio in Art and Architecture; Samuel Obara
[3]. THE GOLDEN RATIO IN THE ARTS
[4].
Back to Gruppe 09