Teaching:TUW - UE InfoVis WS 2007/08 - Gruppe 07 - Aufgabe 1 - Boxplot: Difference between revisions

From InfoVis:Wiki
Jump to navigation Jump to search
No edit summary
No edit summary
Line 9: Line 9:


= Example =
= Example =
As an example we consider values given from the table below to create a histogram (right image). The data derived from the first column of the table shows the class affiliation. According to the table values these classes are aligned along the x-axis of the histogram. Frequenzy values (second column) according to the classes are then printed along the y-axis of the histogram. Once this is properly done, the histogram shows the amount of frequency according to any of the classes. Hence the histogram is a powerful visualisation that can make information accessable in just a few seconds, considering that the table on the left side is representing the same information, it is easy to understand the power of graphical visualisation.
As an example we consider values given from the table below to create a boxplot (right image). Notice that the dataset is approximately balanced around zero. Evidently the mean is near zero. However there is a variation in the dataset which ranges approximately from -6 to 6. The maximum and minimum values are showed as whiskers. Hence it is obvious that the boxplot is a powerful visualisation, that has the ability to outframe characteristic attributes of the given dataset.


<table style="height:16px" border="0">
<table style="height:16px" border="0">
Line 16: Line 16:
   <table style="height:16px" border="1">
   <table style="height:16px" border="1">
<tr>   
<tr>   
<td colspan="2"><b>Data Set</b></td>
<td colspan="2"><b>Dataset</b></td>
</tr>
</tr>
<tr>
<tr>

Revision as of 15:05, 7 November 2007

Definitions

In descriptive statistics, a boxplot (also known as a box-and-whisker diagram or plot or candlestick chart) is a convenient way of graphically depicting groups of numerical data through their five-number summaries (the smallest observation, lower quartile (Q1), median, upper quartile (Q3), and largest observation). A boxplot also indicates which observations, if any, might be considered outliers. The boxplot was invented in 1977 by the American statistician John Tukey.

Boxplots are able to visually show different types of populations, without making any assumptions of the underlying statistical distribution. The spacings between the different parts of the box help indicate variance, skewness and identify outliers. Boxplots can be drawn either horizontally or vertically.
[Wikipedia, 2007]


Read full article on Wikipedia
Boxplot Illustration

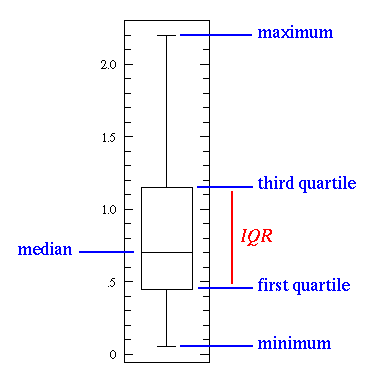
Explanation

TODO PETER ... WEBSTERs ...

Example

As an example we consider values given from the table below to create a boxplot (right image). Notice that the dataset is approximately balanced around zero. Evidently the mean is near zero. However there is a variation in the dataset which ranges approximately from -6 to 6. The maximum and minimum values are showed as whiskers. Hence it is obvious that the boxplot is a powerful visualisation, that has the ability to outframe characteristic attributes of the given dataset.

Dataset
-5.13 -2.19
-2.43 -3.83
0.50 -3.25
4.32 1.63
5.18 -0.43
7.11 4.87
-3.10 -5.81
3.76 6.31
2.58 0.07
5.76 3.50

Related Links

References

Retrieved from "https://infovis-wiki.net/w/index.php?title=Teaching:TUW_-_UE_InfoVis_WS_2007/08_-_Gruppe_07_-_Aufgabe_1_-_Boxplot&oldid=17676"