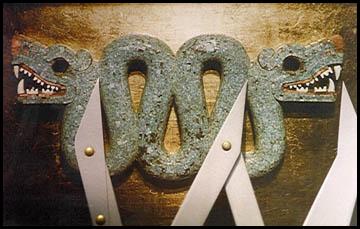Golden Ratio: Difference between revisions

From InfoVis:Wiki
Jump to navigation Jump to search
← Older edit
Ipodsoft (talk | contribs)
11 edits
No edit summary
 
(103 intermediate revisions by 7 users not shown)
Line 4: Line 4:


----
----
===Definition===
===DEFINITION===
The '''golden ratio''' is an irrational mathematical constant with the approximated value of 1.6180339887. It is the relation between two quantities, where the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. [Wikipedia, 2009a]


This mathematical proportion is often recognized as 'aesthetically pleasing', thus it is often found in many different fields like mathematics, architecture, geometry, science, biology, nature, art and design.[Livio, 2002] 


* In the Mathmatics the number 1.61803399 is the golden ratio. [1]
Other names used for the golden ratio are '''golden section''', '''golden mean''', '''extreme and mean ratio''', '''medial section''', '''golden proportion''', '''golden cut''' and  '''golden number'''
[Summerson, 1963]


It is said, that two quantities are in golden ration if and only if the following condition holds:


* Two quantities are said to be in the golden ratio, if "the whole is to the larger as the larger is to the smaller" [2]
[[Image:golden-ratio.png]]


It is mostly symbolised by the Greek letter [[Image:Phi.png]] (phi) or sometimes by the less known τ (tau).


* The golden ratio is sybolised by the Greek letter [[Image:Phi.png]] (phi) and also by the less know τ (tau).
[[Image:golden-ratio-graphical.png|right|thumb|upright|]]


----
The history of the golden ration at least goes back to the ancient greeks, Pythagoras and his followers. The greek mathematician Euclid of Alexandria (365BC - 300BC) first mentioned the '''golden mean'''[Joyce, 1997]:
 
===Introduction===


{{Quotation|A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.| Euclid of Alexandria(ca. 300BC)}}


The use of the golden ratio can be found in many different fields. In mathematics, architecture,  geometry, science, biology, nature, art, design and many others.


Other names of this word are as follows: the '''golden mean''',''' golden section''', '''golden number''', '''divine proportion''' or '''sectio divina'''(golden Cut).
'''Source(s):''' [http://www.downloadranking.com  Golden Ratio calculation tool]


----
----
===History===


===CALCULATION===


The Golden ratio can be found as far back to the building of the Great Pyramid of Giza around  2560 BC.
Method for calculation of golden ratio constant is beginning from the following algebraic formula:


[[Image:golden-ratio.png]]


The actual discovery of the golden ratio can be lead back to the ancient Greeks and the Pythagoras. The greek mathematician Euclid of Alexandria (365BC - 300BC) mentioned the golden mean.
From the formula we obtain that a is equal b/[[Image:Phi.png]], so we can replace all occurences of a:


{{Quotation|... A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser...| Euclid of Alexandria(ca. 300BC)}}
[[Image:golden-ratio-1.png]]


Devided by b formula changes to:


Even Plato, the Greek Philosopher was occupied by the Golden ratio.
[[Image:golden-ratio-2.png]]


----
Now we need to multiply formula by [[Image:Phi.png]] and by moving content of the right side to the left side we get quadratic equation:


===Golden ratio in geometry & mathematics===
[[Image:golden-ratio-3.png]]


The only positive result to above equation is the irrational number we have already presented:


Fibonacci introduced to us, the Fibonacci-Numbers:
[[Image:golden-ratio-4.png]]


1,2,3,5,8,13,21,34,55,89,144,233,377,....


----


Every number of this alignement equals to 0,168 if you divide it with the one before it, and 1,618 when you divide it with the number after it.
===GEOMETRY AND MATHEMATICS===


Fibonacci introduced a sequence of numbers, today called the '''Fibonacci Numbers''', which is often found in natural sciences. By definition, the first two Fibonacci numbers are 0 and 1, and each remaining number is the sum of the previous two [Wikipedia, 2009a] .


These are the relationships between the larger and smaller numbers in the golden ratio.
1,2,3,5,8,13,21,34,55,89,144,233,377,....




Below you can find an example of the Fibonacci-Numbers
Every number of this alignment equals to 0,168 if you divide it with the one before it, and 1,618 when you divide it with the number after it. These are the relationships between the larger and smaller numbers in the golden ratio. Below you can see example for division of bigger by smaller number:


[[Image:fibonacci.jpg]]
[[Image:fibonacci-example-1.png]]


and by smaller devided by bigger number:


[[Image:fibonacci-example-2.png]]


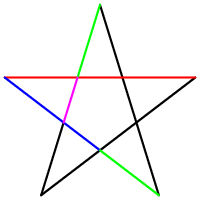
'''The Golden Ratio''' can also be found in different kinds of shapes. This goes on from the usual rechangle, through different kinds of triangles and to the very complicated shapes like the pentacle.


There are many shapes in which golden ratio were discovered. Examples of those you can see on the right side.


A rectanle is a Golden rectangle when the sides are in the 1:0,618 proportion. Below is an example of this kind of shape.
{| cellpadding="1" style="border:1px solid darkgray;"
!width="140"|Pentagram
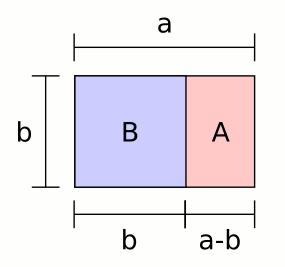
!width="150"|Golden rectangle
|- align=center
| style="border:1px solid;"|
[[Image:Pentagram2.png|120px]]
| style="border:1px solid;"|
[[Image:Golden_rectangle.png|120px]]
|- align=center
|Image Illustrates the hidden golden ratio in the very special shape, '''pentagram'''. || A rectangle is a '''golden rectangle''' when the sides are in the 1:0,618 proportion.
|}


[[Image:Golden_rectangle.png]]


Image 1: Golden Rectangle (Wikipedia: Golden Ratio)
----


===ART & DESIGN===




Another shape where the golden ratio can be found is the Pentagramm. This image below, illustrates the hidden golden ratio in this very special shape.
Since the beginning of ART & Design, the artist and designers used the golden ratio in order to manage and achieve beauty and balance in their creations. In the following table you can see few examples for all.
 
{| cellpadding="2" style="border:1px solid darkgray;"
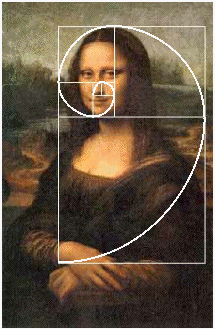
[[Image:Pentagram2.png]]
!width="140"|Mona-Liza
 
!width="150"|Aztek decorations
Image 2: Golden Pentagramm
!width="130"|Credit cards
 
|- align=center
| style="border:1px solid;"|
[[Image:mona-liza.gif]]
| style="border:1px solid;"|
[[Image:aztec.jpg|120px]]
| style="border:1px solid;"|
[[Image:cards.jpg|120px]]
|- align=center
| In Mona-Liza painting you can find many golden rectangles that together create golden spiral.|| The space between the two heads is exacly Phi times the width of the heads.|| if you measure a credit-card, the outcome would be a perfect golden rectangle.
|}


----
----
===Golden ratio in ART & DESIGN===
Since the beginning of ART & Design, the artist and designers used the golden ratio in order to manage and achieve beauty and balance in their creations.
{{Quotation|... Many books claim that if you draw a rechtangle around the face of Leonardo da Vinci's Mona Lisa, the ratio of the height to width of the rectangle is equal to the Golden Ratio ...| Mario Livio; Nov. 2002}}
The evidence of the golden ratio was proved on many different creations, like the Aztek decorations below:


[[Image:aztec.jpg]]
===Architecture===


The space between the two heads is exacly Phi times the width of the heads. [4]
There is many examples of golden ratio even in architecture. Architect were inspired by this "sacred ratio" already in times of Pyramids. Even in Greek you can find golden rectangles, spirals, etc. In the table below you can find several examples.




The California Polytechnic State University is planing to build a new Engineering Plaza. This new construction is based on the Fibonacci numbers. The whole plan also bases on some shapes, which can be used to show the meaning of the golden ratio. The Designers of this new Plaza have chosen the Fibonacci series spiral, or also called the golden mean to design this new state of the art plaza. Below you can see, what the plaza should look like:
{| cellpadding="2" style="border:1px solid darkgray;"
 
!width="140"|Great Pyramid of Giza
 
!width="150"|Parthenon
[[Image:polyplaza.jpg]]
!width="130"|Engineering Plaza
 
|- align=center
California Polytechnic Engineering Plaza [5]
| style="border:1px solid;"|
 
[[Image:great-pyramid.gif]]
 
| style="border:1px solid;"|
Even the mountainbike shown below, has the golden ratio built in. Take a look at the image, and the marked golden sections of the bike.
[[Image:parthenon.gif|120px]]
 
| style="border:1px solid;"|
 
[[Image:polyplaza.jpg|120px]]
[[Image:bike.jpg]]
|- align=center
 
| The Great Pyramid has proportions designed according to golden ratio.[Obara, 2000]|| Even in proportions of Parthenon you can find golden spiral consisting of golden rectangles.[Obara, 2000]|| The Designers of this new Plaza have chosen the Fibonacci series spiral, or also called the golden mean to design this new state of the art plaza.[Knott, 2009]
Mountainbike Trek Fuel 90 (belongs to Brian Agron of Fairfax)[5]
|}
 
 
So the use of the golden ratio can not only be found in ancient paintings and sculptures, but also in the stunning creations still to come.
 
Did you know, that if you measure a credit-card, the outcome would be a perfect golden rectangle. This ofcourse shows, that the golden ratio is very well in use. Even if it comes to the proportions and masses of everyday things like credit cards.
 
 
[[Image:card.jpg]]
 
Credit Cards [6]




----
----


==Resources==
== Related Links ==
 
*[http://www.goldenmeangauge.co.uk/fibonacci.htm The Fibonacci Series]
 
*[http://www.golden-section.eu Der goldene Schnitt - Das Mysterium der Schönheit]
[1]. Wikipedia.org: Golden Ratio
[Wikipedia, Golden Ratio, 2005] Wikipedia.org, Golden Ratio, 19.10.2005, http://en.wikipedia.org/wiki/Golden_ratio
 
[Wikipedia, Golden rectangle, 2005] Wikipedia.org, Golden rectangle, 24.10.2005, http://en.wikipedia.org/wiki/Golden_rectangle
* http://en.wikipedia.org/wiki/Golden_ratio
[Wikipedia, Pentagram, 2005] Wikipedia.org, Pentagram, 29.10.2005, http://en.wikipedia.org/wiki/Pentagram
 
 
[2]. Golden Ratio:
 
* http://www.absoluteastronomy.com/encyclopedia/g/go/golden_ratio.htm
 
 
[3]. University of Georgia: Golden Ratio in Art and Architecture; Samuel Obara
 
* http://jwilson.coe.uga.edu/EMT668/EMAT6680.2000/Obara/Emat6690/Golden%20Ratio/golden.html
 
 
[4]. THE GOLDEN RATIO IN THE ARTS
 
* http://students.bath.ac.uk/ma1caab/art.html
 
 
[5]. Fibonacci Numbers and The Golden Section in Art, Architecture and Music
 
* http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibInArt.html
 
[6]. Credit Cards
 
* http://www.batterywholesaler.co.uk/battery_images/
 
 
----
----


Back to [[Teaching:TUW - UE InfoVis WS 2005/06 - Gruppe 09|Gruppe 09]]


Back to [[Teaching:TUW - UE InfoVis WS 2005/06|Teaching:TUW - UE InfoVis WS 2005/06 ]]
I am.  But you're confusing the deerins with that word.  They don't understand what a consensus is or isn't or how they come to exist.Besides, don't you know that every scientific organization is made up of weak-kneed scientists who are spreading fairytales and that leftist alarmists like to tell them to small children to frighten them.You know  Like Bigfoot.Dax  *sigh*  You know nothing of science.  Look up "falsifiability".  Besides that, if you want to use legalese, you have the burden of proof since you are the one crying foul.  If you initiate a case (such as AGW is a socialist plot to implement the NWO), you are considered the plaintiff and assume the burden of proof.  In other words, *YOU* need to back up *YOUR* claims as scientists already back up theirs in the scientific literature I'm sorry richie, but not a single one of your examples is relevant to the question.  Though when you use the Einstein quote, you may want practice some introspection.You may also want to stop plagiarizing.  It's illegal, you know?_

Latest revision as of 05:53, 22 November 2012

GOLDEN RATIO

DEFINITION

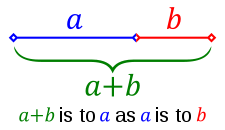
The golden ratio is an irrational mathematical constant with the approximated value of 1.6180339887. It is the relation between two quantities, where the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. [Wikipedia, 2009a]

This mathematical proportion is often recognized as 'aesthetically pleasing', thus it is often found in many different fields like mathematics, architecture, geometry, science, biology, nature, art and design.[Livio, 2002]

Other names used for the golden ratio are golden section, golden mean, extreme and mean ratio, medial section, golden proportion, golden cut and golden number [Summerson, 1963]

It is said, that two quantities are in golden ration if and only if the following condition holds:

It is mostly symbolised by the Greek letter (phi) or sometimes by the less known τ (tau).

The history of the golden ration at least goes back to the ancient greeks, Pythagoras and his followers. The greek mathematician Euclid of Alexandria (365BC - 300BC) first mentioned the golden mean[Joyce, 1997]:

A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.
Euclid of Alexandria(ca. 300BC)



Source(s): Golden Ratio calculation tool

CALCULATION

Method for calculation of golden ratio constant is beginning from the following algebraic formula:

From the formula we obtain that a is equal b/, so we can replace all occurences of a:

Devided by b formula changes to:

Now we need to multiply formula by and by moving content of the right side to the left side we get quadratic equation:

The only positive result to above equation is the irrational number we have already presented:


GEOMETRY AND MATHEMATICS

Fibonacci introduced a sequence of numbers, today called the Fibonacci Numbers, which is often found in natural sciences. By definition, the first two Fibonacci numbers are 0 and 1, and each remaining number is the sum of the previous two [Wikipedia, 2009a] .

1,2,3,5,8,13,21,34,55,89,144,233,377,....


Every number of this alignment equals to 0,168 if you divide it with the one before it, and 1,618 when you divide it with the number after it. These are the relationships between the larger and smaller numbers in the golden ratio. Below you can see example for division of bigger by smaller number:

and by smaller devided by bigger number:


There are many shapes in which golden ratio were discovered. Examples of those you can see on the right side.

Pentagram Golden rectangle

Image Illustrates the hidden golden ratio in the very special shape, pentagram. A rectangle is a golden rectangle when the sides are in the 1:0,618 proportion.


ART & DESIGN

Since the beginning of ART & Design, the artist and designers used the golden ratio in order to manage and achieve beauty and balance in their creations. In the following table you can see few examples for all.

Mona-Liza Aztek decorations Credit cards

In Mona-Liza painting you can find many golden rectangles that together create golden spiral. The space between the two heads is exacly Phi times the width of the heads. if you measure a credit-card, the outcome would be a perfect golden rectangle.

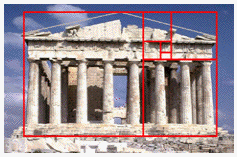
Architecture

There is many examples of golden ratio even in architecture. Architect were inspired by this "sacred ratio" already in times of Pyramids. Even in Greek you can find golden rectangles, spirals, etc. In the table below you can find several examples.


Great Pyramid of Giza Parthenon Engineering Plaza

The Great Pyramid has proportions designed according to golden ratio.[Obara, 2000] Even in proportions of Parthenon you can find golden spiral consisting of golden rectangles.[Obara, 2000] The Designers of this new Plaza have chosen the Fibonacci series spiral, or also called the golden mean to design this new state of the art plaza.[Knott, 2009]


Related Links

[Wikipedia, Golden Ratio, 2005] Wikipedia.org, Golden Ratio, 19.10.2005, http://en.wikipedia.org/wiki/Golden_ratio [Wikipedia, Golden rectangle, 2005] Wikipedia.org, Golden rectangle, 24.10.2005, http://en.wikipedia.org/wiki/Golden_rectangle [Wikipedia, Pentagram, 2005] Wikipedia.org, Pentagram, 29.10.2005, http://en.wikipedia.org/wiki/Pentagram


I am. But you're confusing the deerins with that word. They don't understand what a consensus is or isn't or how they come to exist.Besides, don't you know that every scientific organization is made up of weak-kneed scientists who are spreading fairytales and that leftist alarmists like to tell them to small children to frighten them.You know Like Bigfoot.Dax *sigh* You know nothing of science. Look up "falsifiability". Besides that, if you want to use legalese, you have the burden of proof since you are the one crying foul. If you initiate a case (such as AGW is a socialist plot to implement the NWO), you are considered the plaintiff and assume the burden of proof. In other words, *YOU* need to back up *YOUR* claims as scientists already back up theirs in the scientific literature I'm sorry richie, but not a single one of your examples is relevant to the question. Though when you use the Einstein quote, you may want practice some introspection.You may also want to stop plagiarizing. It's illegal, you know?_

Retrieved from "https://infovis-wiki.net/w/index.php?title=Golden_Ratio&oldid=147777"