Teaching:TUW - UE InfoVis WS 2007/08 - Gruppe 07 - Aufgabe 1 - Histogram: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (36 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
= Definitions = | = Definitions = | ||
{{Quotation| In statistics, a <b>histogram</b> is a graphical display of tabulated frequencies. A histogram is the graphical version of a table that shows what proportion of cases fall into each of several or many specified categories. The histogram differs from a bar chart in that it is the area of the bar that denotes the value, not the height, a crucial distinction when the categories are not of uniform width | {{Quotation| In statistics, a <b>histogram</b> is a graphical display of tabulated frequencies. A histogram is the graphical version of a table that shows what proportion of cases fall into each of several or many specified categories. The histogram differs from a bar chart in that it is the area of the bar that denotes the value, not the height, a crucial distinction when the categories are not of uniform width. |[Lancaster, 1974]}} | ||
{{Quotation|A <b>histogram</b> is used when we want to show frequencies of a continous variable. The continous variable can, of course, assume all values within an interval and the histogram reflects this by covering the whole of the interval concerned.|[Wallgreen et al., 1996]}} | {{Quotation|A <b>histogram</b> is used when we want to show frequencies of a continous variable. The continous variable can, of course, assume all values within an interval and the histogram reflects this by covering the whole of the interval concerned.|[Wallgreen et al., 1996]}} | ||
= Explanation = | = Explanation = | ||
For drawing the histogram, the numerical values are first put in ascending order. Then the data field is split into j classes. | |||
Each class has a defined width (class interval) - normally it is 1, but in special cases it is useful to choose a width > 1 - e.g. for displaying frequencies concerning distinct age groups. Under "Examples" we consider a histogram of varying class intervals. | |||
= Example = | = Example = | ||
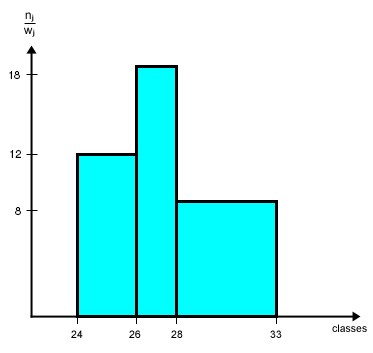
As an example we consider values given from the table below to create a histogram (right image). The data derived from the first column of the table shows the class affiliation. According to the table values these classes are aligned along the x-axis of the histogram. | |||
As an example we consider values given from the table below to create a histogram (right image). The data derived from the first column of the table shows the class affiliation. According to the table values these classes are aligned along the x-axis of the histogram. The heigth of each histogram bar (frequency density) can be obtained by dividing the absolute frequenzy values (second column) by the corresponding class intervals. The resulting value of each class is then printed along the y-axis of the histogram. Once this is properly done, the histogram shows the amount of frequency according to any of the classes. Hence the histogram is a powerful visualisation that can make information accessable in just a few seconds, considering that the table on the left side is representing the same information, it is easy to understand the power of graphical visualisation. | |||
<table style="height:16px" border="0"> | <table style="height:16px" border="0"> | ||
<tr> | <tr> | ||
<td><table style="height:16px" border="1"> | <td><table style="height:16px; text-align:center;" border="1" align="top"> | ||
<b>Frequency | <b>Frequency density</b> (height of a column) = n <sub> j </sub> / w <sub> j </sub> <br /> | ||
<b>Frequency (area)</b> = Width x Height <br /><br /> | |||
<th>class j</th> | <th>class j</th> | ||
<th>absolute frequency n<sub>j</sub></th> | <th>absolute frequency n<sub>j</sub></th> | ||
| Line 36: | Line 39: | ||
</table></td> | </table></td> | ||
<td>[[image:histogram_sample.jpg|thumb|200px|right|Histogram Illustration]]</td> | <td>[[image:histogram_sample.jpg|thumb|200px|right|Histogram Illustration]]</td> | ||
<tr> | <tr></table> | ||
</table | |||
= Related Links = | = Related Links = | ||
*[http://en.wikipedia.org/wiki/Histogram ''Definition of Histogram on Wikipedia''] | |||
*[http://www.luminous-landscape.com/tutorials/understanding-series/understanding-histograms.shtml ''Understanding Histograms in digital photography''] | *[http://www.luminous-landscape.com/tutorials/understanding-series/understanding-histograms.shtml ''Understanding Histograms in digital photography''] | ||
*[http://www.shodor.org/interactivate/activities/histogram/ ''Histogram applet''] | |||
= References = | = References = | ||
*[ | *[Lancaster, 1974] H.O. Lancaster, An Introduction to Medical Statistics. John Wiley and Sons. 1974. ISBN 0 471 51250-8 | ||
*[Wallgreen et al., 1996] Anders Wallgreen, Britt Wallgreen, Rolf Persson, Ulf Jorner and Jan-Aage Haaland. Graphing Statistics & Data: Creating Better Charts. SAGE Publications, Thousand Oaks, London, New Delhi, 1996. | *[Wallgreen et al., 1996] Anders Wallgreen, Britt Wallgreen, Rolf Persson, Ulf Jorner and Jan-Aage Haaland. Graphing Statistics & Data: Creating Better Charts. SAGE Publications, Thousand Oaks, London, New Delhi, 1996. | ||
*[Evans, 2004] Geraint Evans, Histograms. [http://www.censusatschool.ntu.ac.uk/ ''CensusAtScool'']. Retrieved at: November 08, 2007. http://www.censusatschool.ntu.ac.uk/files/histogram.pdf | |||
Latest revision as of 19:19, 1 December 2007
Definitions[edit]
In statistics, a histogram is a graphical display of tabulated frequencies. A histogram is the graphical version of a table that shows what proportion of cases fall into each of several or many specified categories. The histogram differs from a bar chart in that it is the area of the bar that denotes the value, not the height, a crucial distinction when the categories are not of uniform width.
[Lancaster, 1974]
A histogram is used when we want to show frequencies of a continous variable. The continous variable can, of course, assume all values within an interval and the histogram reflects this by covering the whole of the interval concerned.
[Wallgreen et al., 1996]
Explanation[edit]
For drawing the histogram, the numerical values are first put in ascending order. Then the data field is split into j classes. Each class has a defined width (class interval) - normally it is 1, but in special cases it is useful to choose a width > 1 - e.g. for displaying frequencies concerning distinct age groups. Under "Examples" we consider a histogram of varying class intervals.
Example[edit]
As an example we consider values given from the table below to create a histogram (right image). The data derived from the first column of the table shows the class affiliation. According to the table values these classes are aligned along the x-axis of the histogram. The heigth of each histogram bar (frequency density) can be obtained by dividing the absolute frequenzy values (second column) by the corresponding class intervals. The resulting value of each class is then printed along the y-axis of the histogram. Once this is properly done, the histogram shows the amount of frequency according to any of the classes. Hence the histogram is a powerful visualisation that can make information accessable in just a few seconds, considering that the table on the left side is representing the same information, it is easy to understand the power of graphical visualisation.
Frequency density (height of a column) = n j / w j
|
 |
||||||||||||
Related Links[edit]
- Definition of Histogram on Wikipedia
- Understanding Histograms in digital photography
- Histogram applet
References[edit]
- [Lancaster, 1974] H.O. Lancaster, An Introduction to Medical Statistics. John Wiley and Sons. 1974. ISBN 0 471 51250-8
- [Wallgreen et al., 1996] Anders Wallgreen, Britt Wallgreen, Rolf Persson, Ulf Jorner and Jan-Aage Haaland. Graphing Statistics & Data: Creating Better Charts. SAGE Publications, Thousand Oaks, London, New Delhi, 1996.
- [Evans, 2004] Geraint Evans, Histograms. CensusAtScool. Retrieved at: November 08, 2007. http://www.censusatschool.ntu.ac.uk/files/histogram.pdf