Hyperbolic trees: Difference between revisions
Jacintheford (talk | contribs) No edit summary |
|||
| (20 intermediate revisions by 6 users not shown) | |||
| Line 27: | Line 27: | ||
== Examples and use cases == | == Examples and use cases == | ||
[[Image:Roget2000.jpg|thumb|Visualization of Roget Thesaurus using the IV XML Toolkit. ]] | |||
Hyperbolic trees are often used to display webinformation. Therefore hyperbolic browsers were developed which support effective interaction with much lager hierarchies than conventional hierarchy viewers and complements the strengths of other novel tree browsers. | Hyperbolic trees are often used to display webinformation. Therefore hyperbolic browsers were developed which support effective interaction with much lager hierarchies than conventional hierarchy viewers and complements the strengths of other novel tree browsers. | ||
| Line 37: | Line 37: | ||
So the big advantage of hyperbolic tree browsers is the possibility to display a big amount of hierarchical information within a small space without a loss of focus and context. | So the big advantage of hyperbolic tree browsers is the possibility to display a big amount of hierarchical information within a small space without a loss of focus and context. | ||
== References == | == References == | ||
[Lamping, et al., 1995] John Lamping, Ramana Rao, Peter Pirolli, A Focus | [Lamping, et al., 1995] John Lamping, Ramana Rao, Peter Pirolli, A Focus Context Technique Based on Hyperbolic Geometry for Visualizing Large Hierarchies, Xerox Palo Alto Research Center, Last Retrieved at: April 27, 2006. http://www.acm.org/sigchi/chi95/Electronic/documnts/papers/jl_bdy.htm | ||
* [http://www.papdan.com/ Melbourne Web Developer] | |||
* [http://www.papdan.com/services/search-engine-optimization/ Melbourne SEO Services] | |||
* [http://www.phillro.com.au/product-category/industrial-spray-equipment/airless-spray-packages/ Airless Spray] | |||
* [http://www.phillro.com.au/product-category/industrial-spray-equipment/spray-guns/ Spray Gun] | |||
* [http://www.oxone-online.com Oxone] | |||
Latest revision as of 09:43, 6 October 2017
Authors
Short Description
Suitable Datatypes
This visualization method can be used on hierarchies. With its characteristics the method is especially suitable for the visualization and manipulation of large hierachical data.
Figures
The Circle Limit IV 1960 woodcut in black and ocre, printed from 2 blocks by Maurits Cornelis Escher (1898-1972) was the original inspiration for the hyperbolic browser.
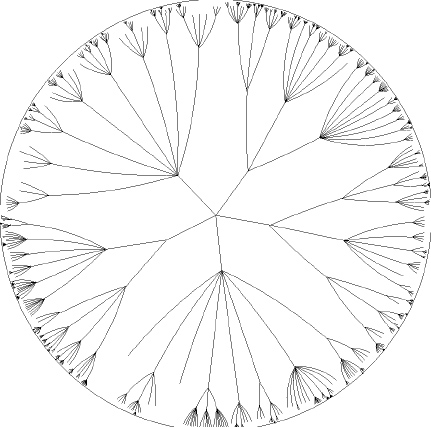
The hyperbolic browser shows a tree of hierarchical information with its root initially in the center, but the display can be transformed to bring other nodes into focus. The following figure shows an original hyperbolic tree with its origin in the center and 1004 nodes:
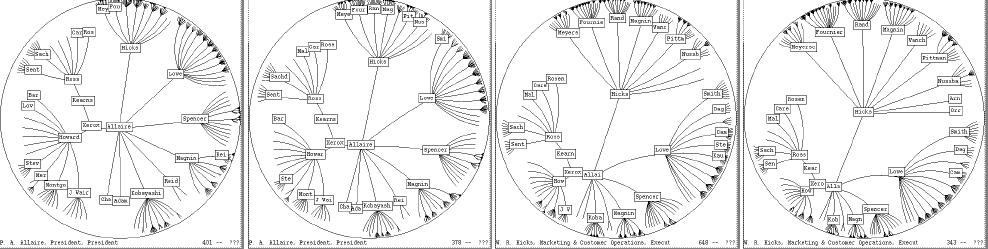
The origin does not have to be in the center of the fisheye as written above. The focus can be changed by the user either by clicking on any visible point to bring it into focus at the center or by dragging any visble point interactively to any other position:
Examples and use cases

Hyperbolic trees are often used to display webinformation. Therefore hyperbolic browsers were developed which support effective interaction with much lager hierarchies than conventional hierarchy viewers and complements the strengths of other novel tree browsers.
Comparison:
If you have a window of 600x600px a standard 2d-hierarchy browser can usually display 100 with 3 character text strings. The hyperbolic browser can display 1000 nodes in this area and about the 50 nearest to the focus can display from 3 up to dozens of characters of text.
So the big advantage of hyperbolic tree browsers is the possibility to display a big amount of hierarchical information within a small space without a loss of focus and context.
References
[Lamping, et al., 1995] John Lamping, Ramana Rao, Peter Pirolli, A Focus Context Technique Based on Hyperbolic Geometry for Visualizing Large Hierarchies, Xerox Palo Alto Research Center, Last Retrieved at: April 27, 2006. http://www.acm.org/sigchi/chi95/Electronic/documnts/papers/jl_bdy.htm