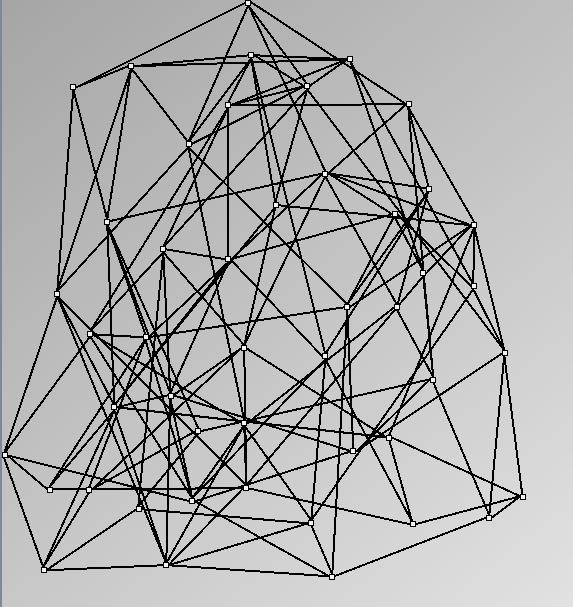
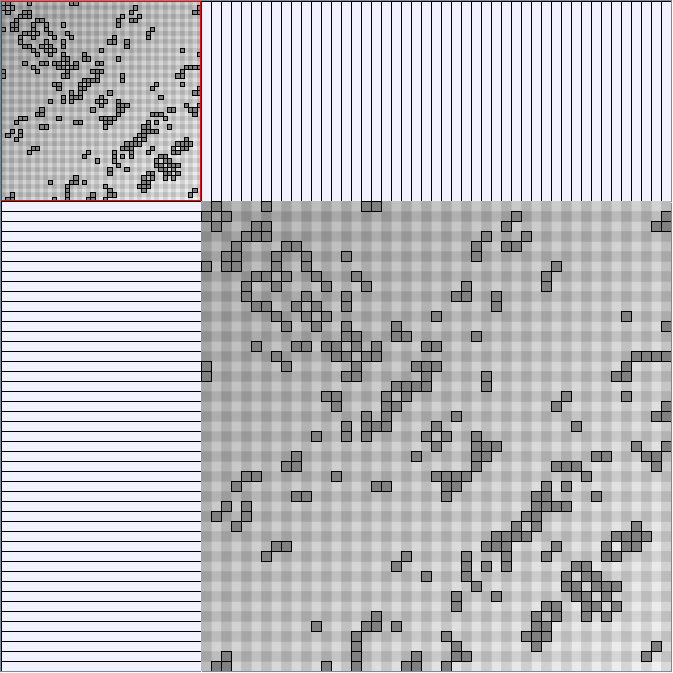
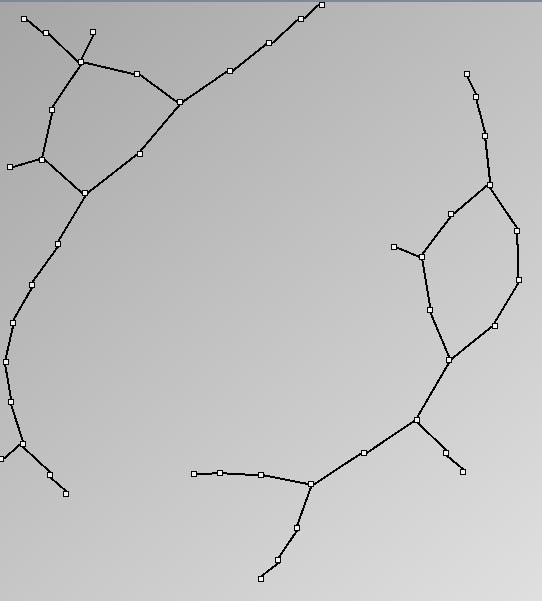
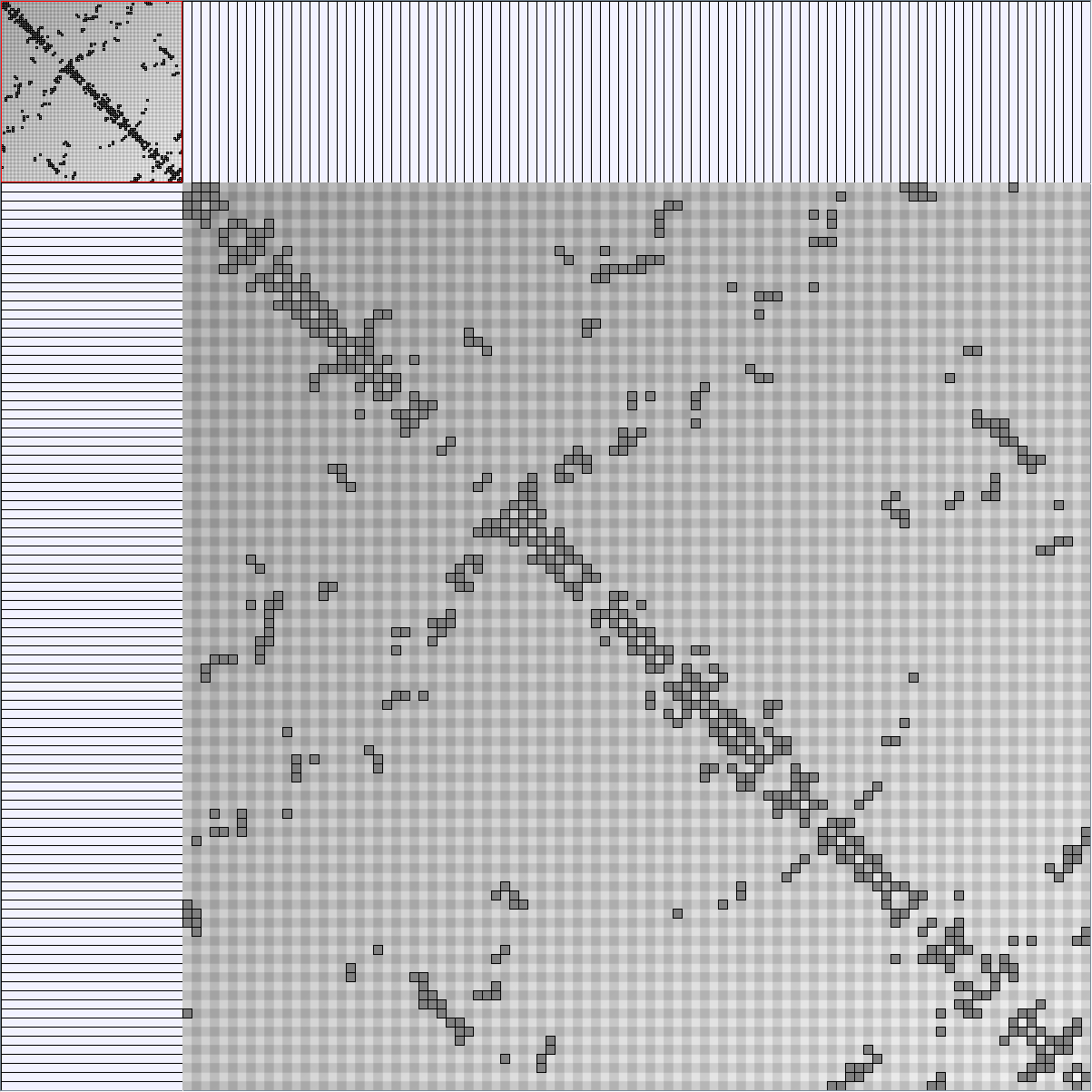
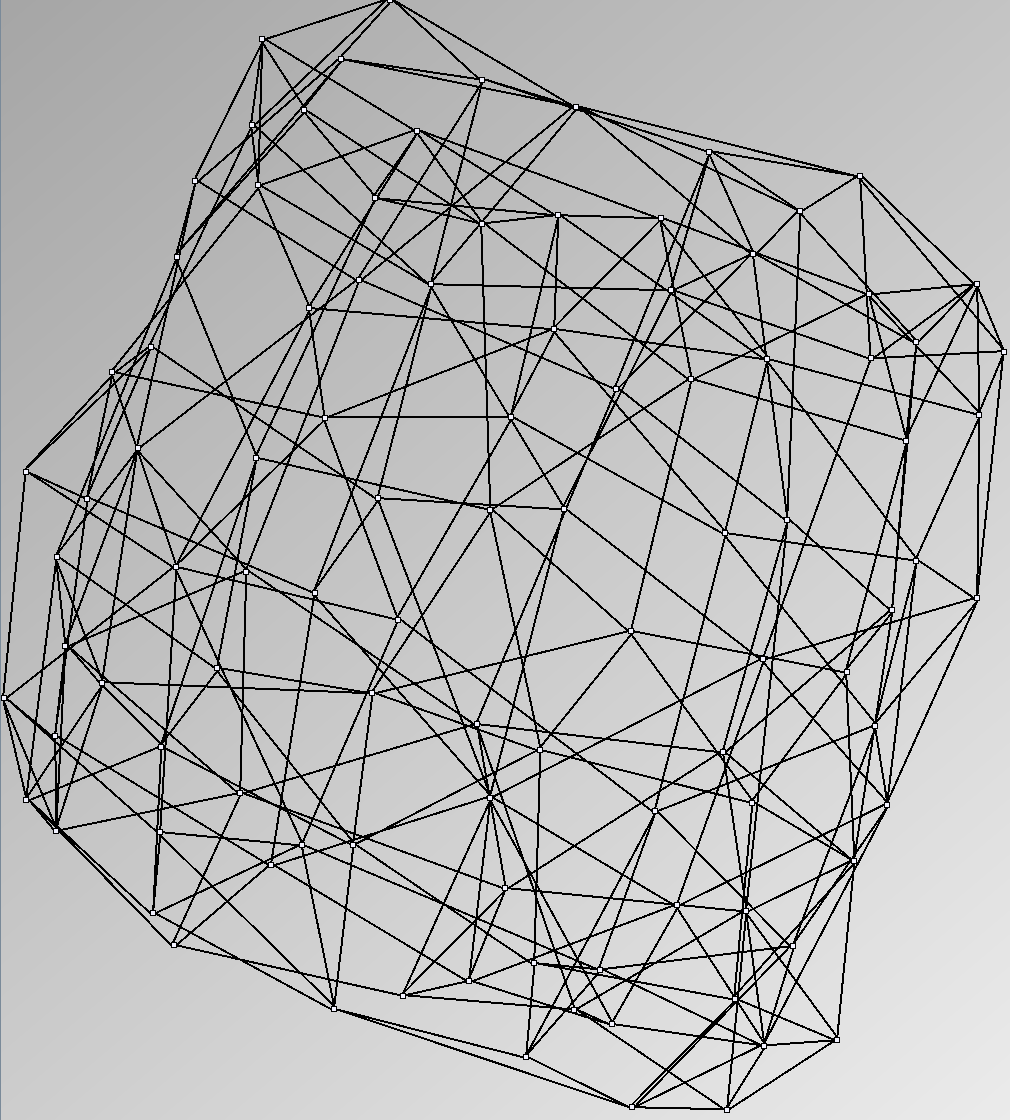
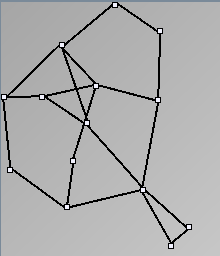
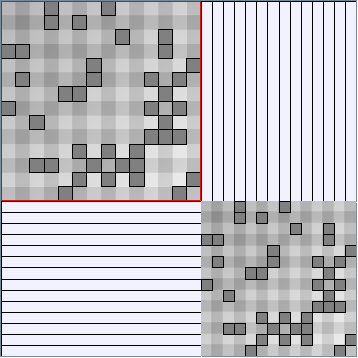
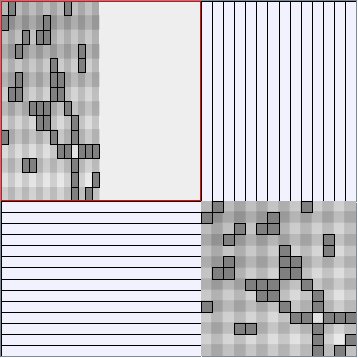
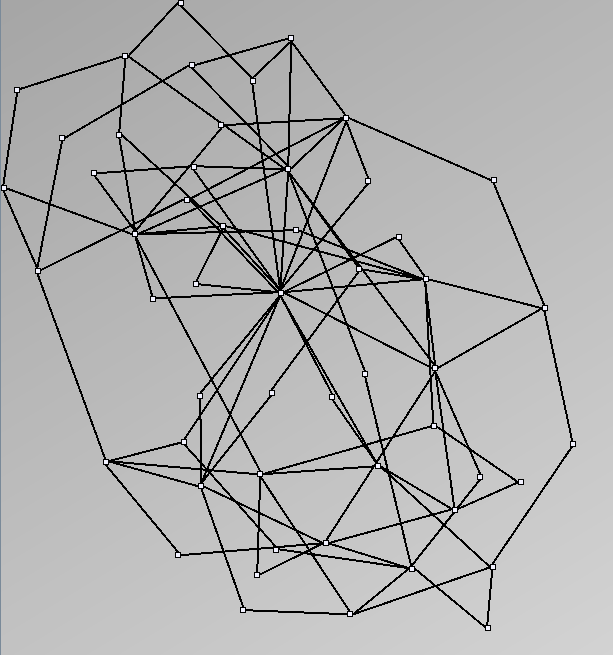
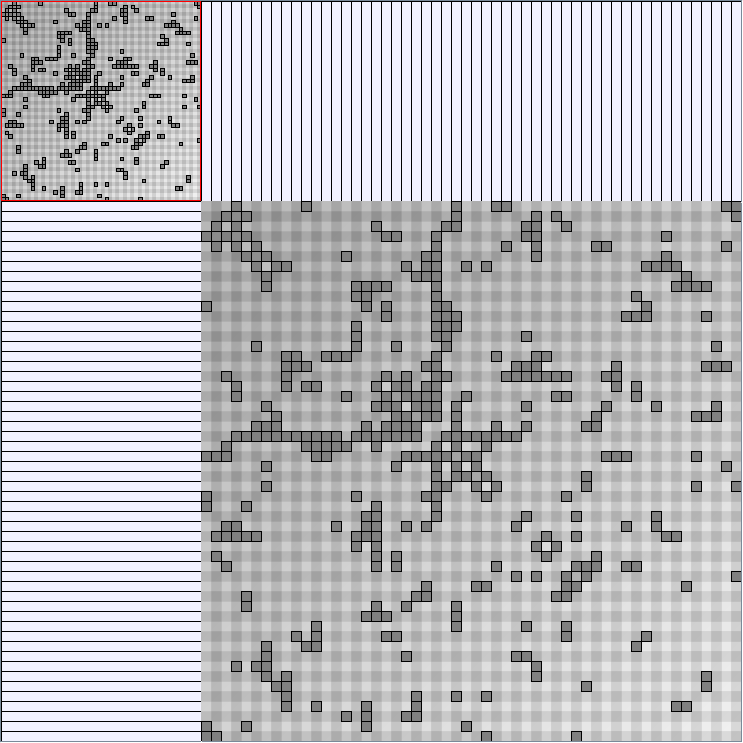
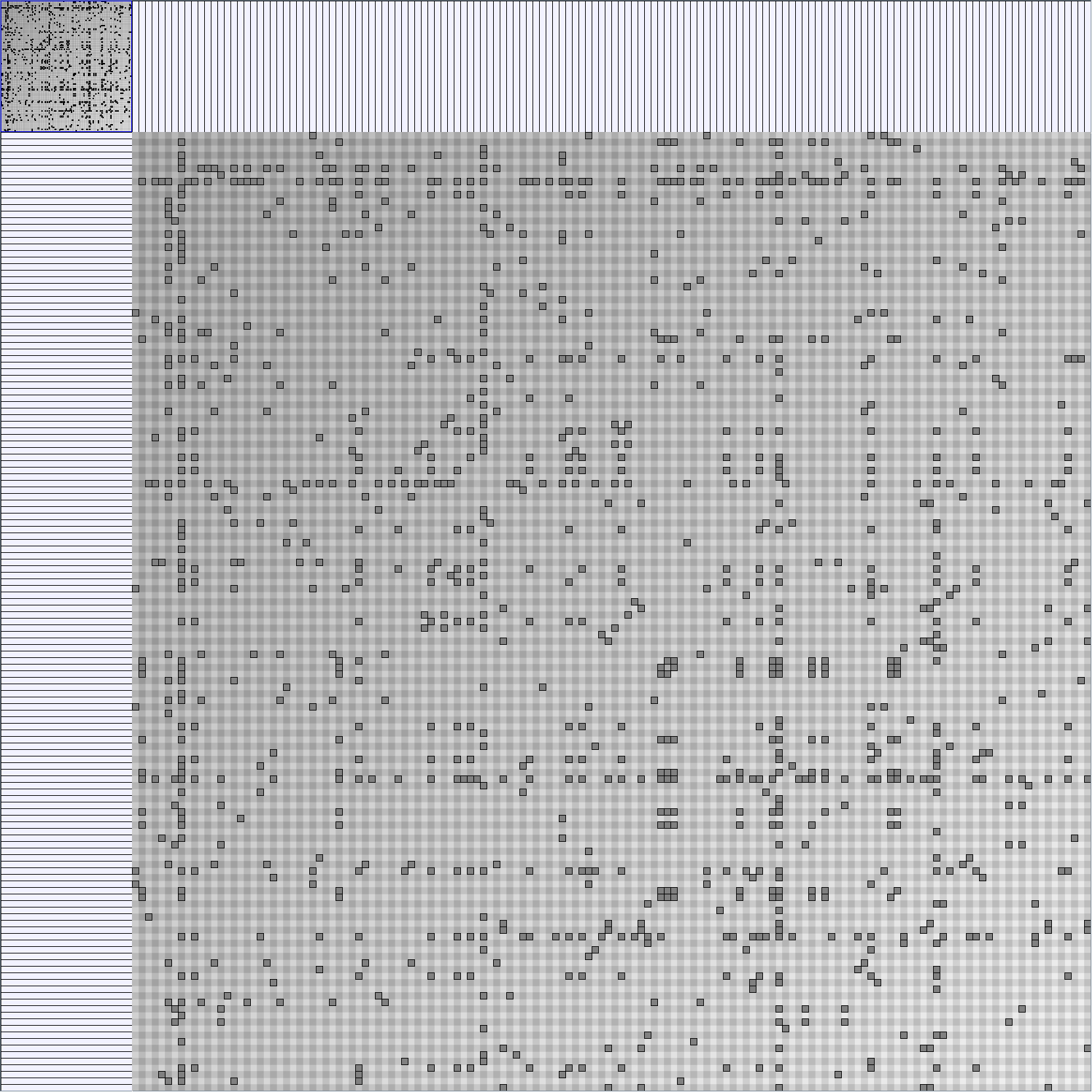
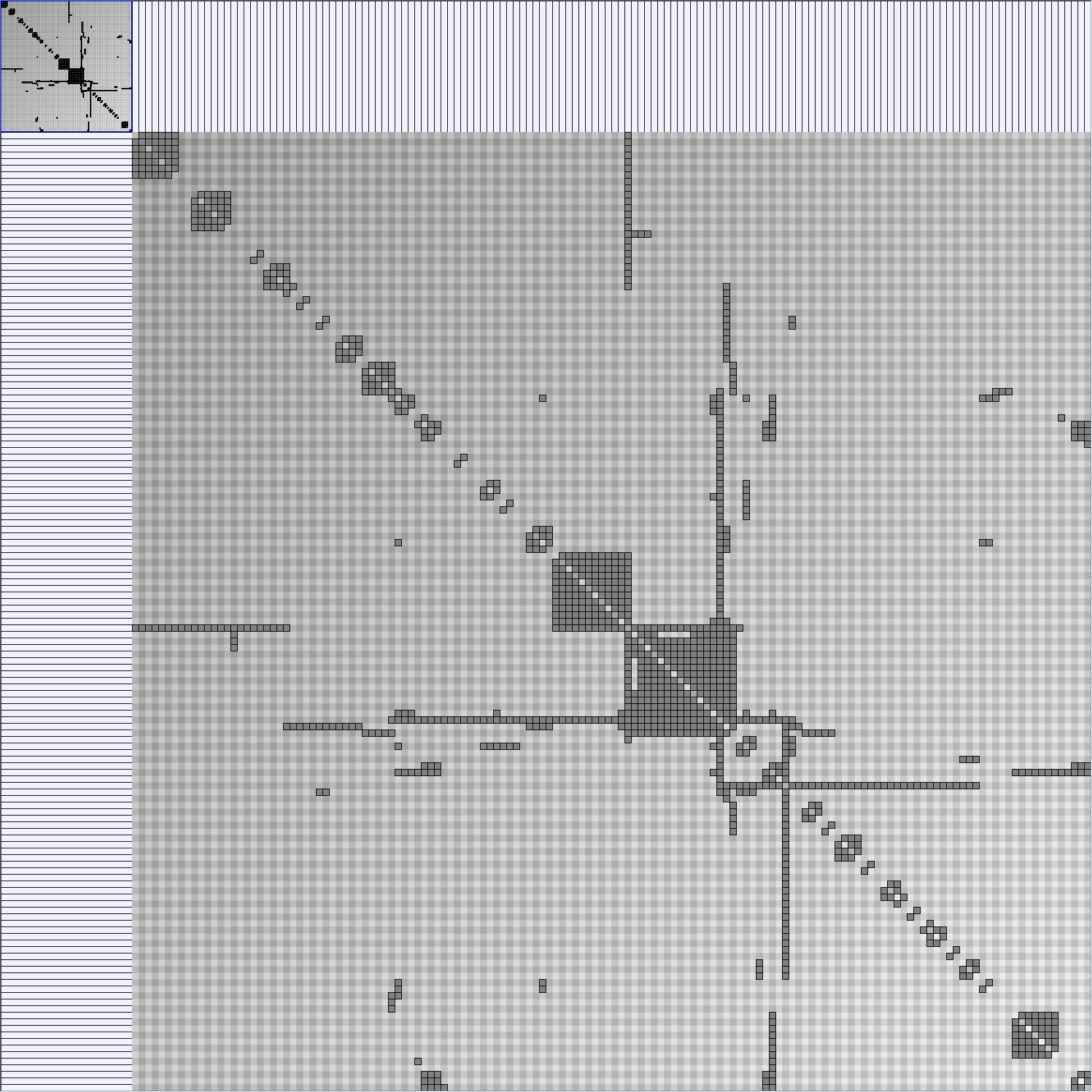
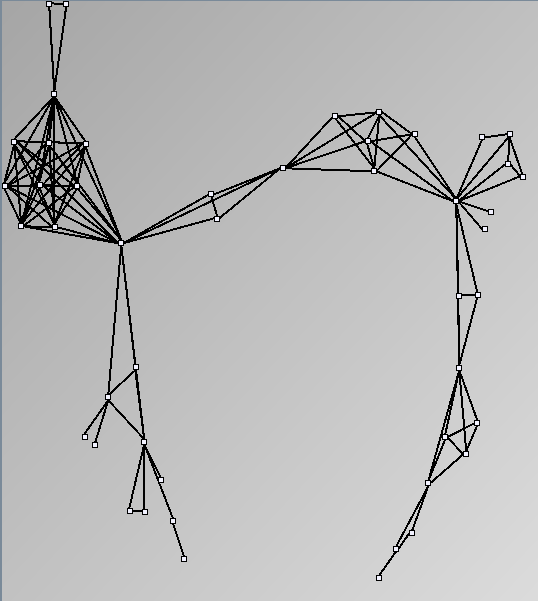
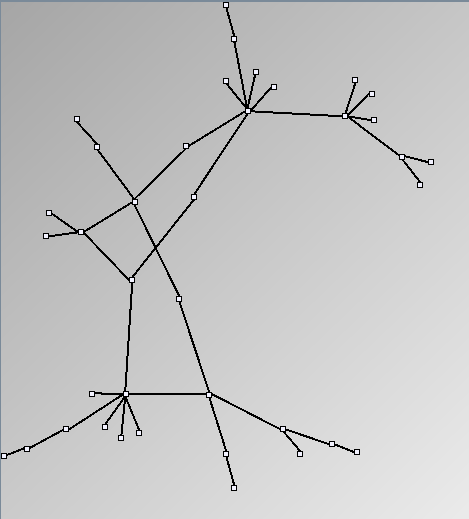
Social Network Generation

This wiki page is under construction...

Research work and images have been realised by Nathalie Henry and Jean-Daniel Fekete, using MatrixExplorer, built with the Infovis Toolkit.

Social Network Characterization

Social networks involve persons or groups called actors and relationship between them, with a lot of variety in the kind of actors and relationships. As described in Wasserman and Faust, actors can be people, subgroups, organizations or collectivities; relations may be friendship (relationships), interactions, communications, transactions, movement or kinship. However, the nature of actors and relations does not really matter: we focus on their structure. We can classify the social networks studied in the literature in three categories:

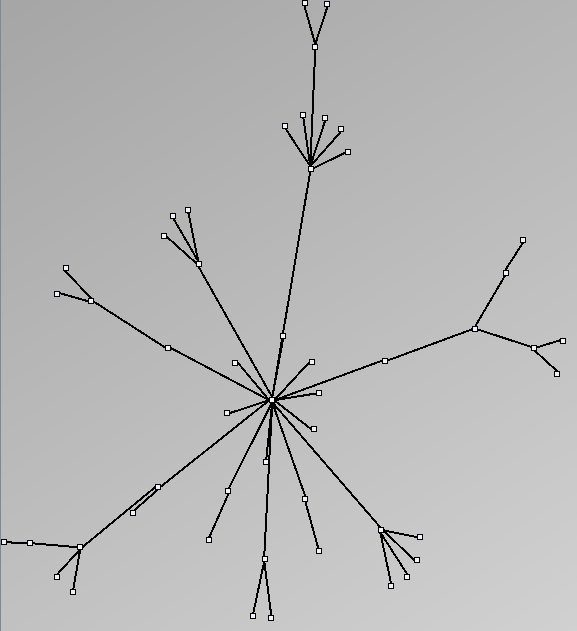
Tree-like are trees with additional links forming cycles with a specified probability. This category includes genealogy data and very sparse graphs such as Sexually-Transmitted Disease (STD) transmission patterns. We call them “almost trees” because they have are mostly acyclic and nodes have very few parents.
Almost complete graphs are complete graphs with missing relations. For example, data about trade between countries, cities or companies are almost complete graphs. They are interesting to study as valued graphs; since they usually carry values on their edges.
Small-world networks (also scale-free or power-law degree-distribution networks) have been studied intensely since they were first described in Watts and Strogatz. They defined them as graphs with three properties: power-law degree distribution, high clustering coefficient and small average shortest path. They are locally dense (sparse with dense sub-graphs).

Three methods exist to select datasets for assessing the quality of analysis systems in the context of social networks: selecting one or two real datasets hoping they are representative, selecting several datasets or generating random datasets with well-known characteristics shared by social networks. With this last method, one should generate datasets with a controlled set of properties and evaluate the systems knowing the properties in advance. It should then eliminate biases linked to a particular dataset and eases the replication of experiments. Unfortunately, while generating tree-like and almost-complete graphs is relatively straightforward, generating graphs with a small-world network structure is still a research topic for computer scientists and physicists. This page shows the results of popular and available network generators. In light of the real social networks we present in the #Real Social Networks, we consider them unsuitable for evaluations since users can easily notice their artifical nature.

Issues on Social Network Generation for Evaluating Visualizations

Watts and Strogatz first described in (Watts, D. J. and S. H. Strogatz (1998). "Collective dynamics of 'small-world' networks." Nature 393: 440 - 442) the concept of small-world networks. They formalized these networks as graphs with three properties: power-law degree distribution, high clustering coefficient and small average shortest path. In the same paper they propose a basic model fitting these properties consisting in a grid (fixed local neighborhood) with additional links simulating some unexpected relations support to the six degrees of separation discovered by Milgram (Milgram, S. (1967). "The small world problem." Psychology Today: 60-67). Barabási and Albert proposed an incremental model to improve it (Barabási, A.-L. and R. Albert (1999). "Emergence of Scaling in Random Networks." Science 286(5439): 509 - 512. ). Since Watts and Strogatz’ model, several have been proposed each generating networks with one or two of the described properties (power-law) but none combine the three of them.

Here are some results of available generators present in the JUNG package. Let's note that for each network generated we only keep the biggest component. Generators present in Pajek[1] and Geomi[2] are incremental scale-free networks generators such as the Barabasi and Albert model.

About datasets and representations

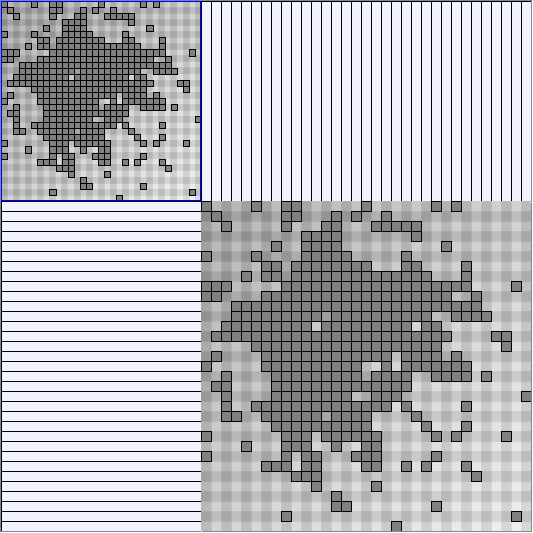
All datasets are downloadable in GraphMl format.
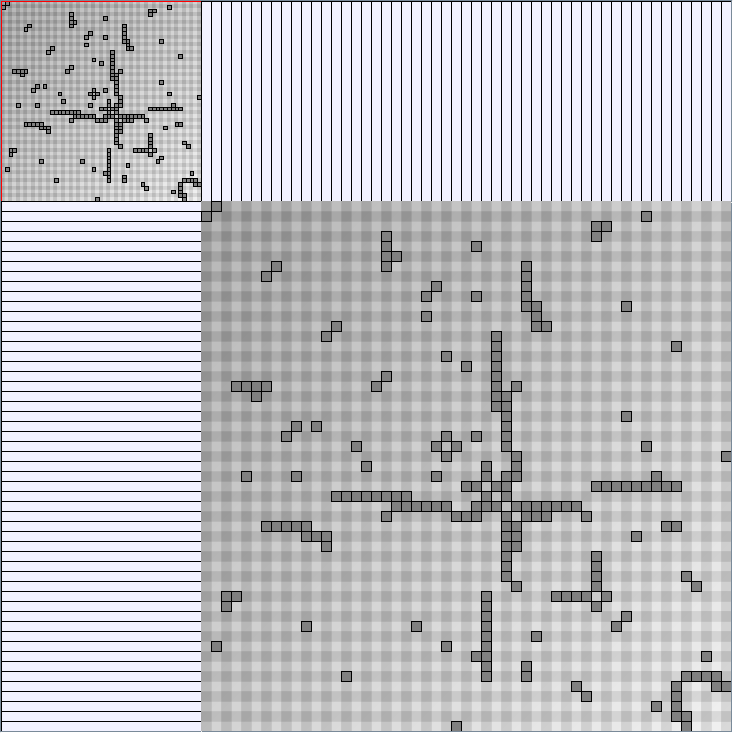
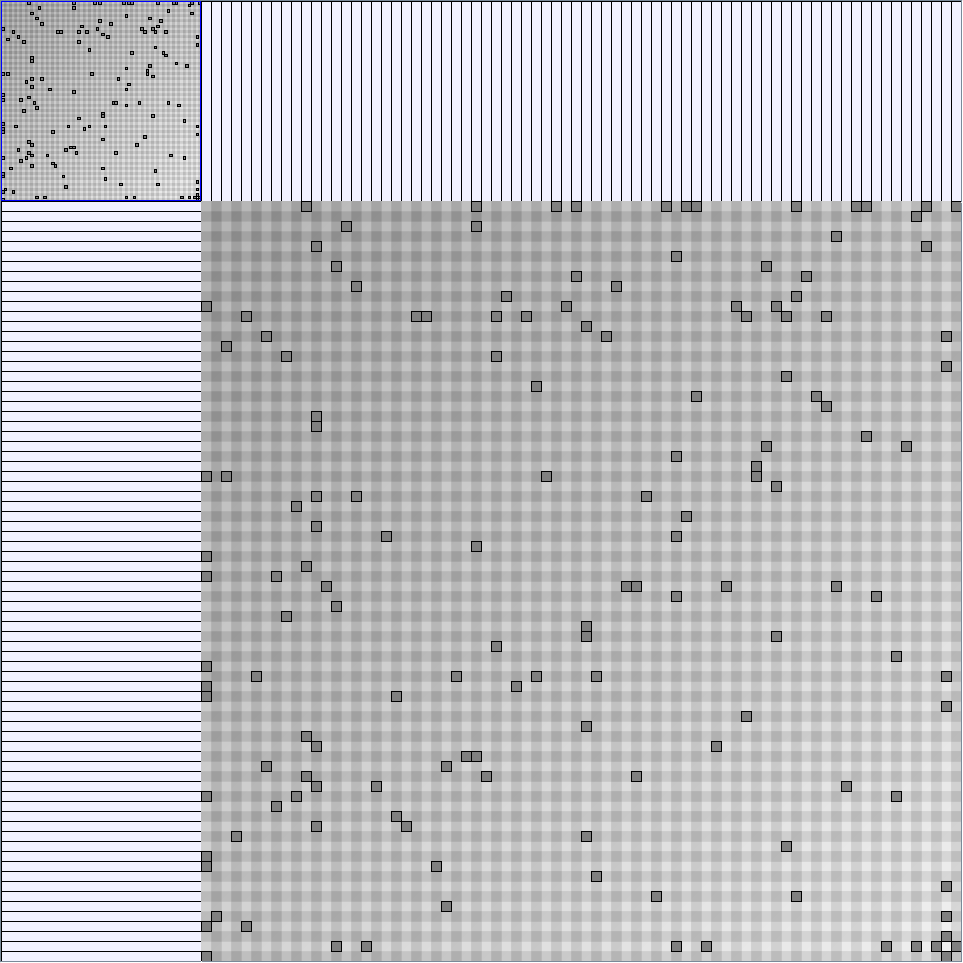
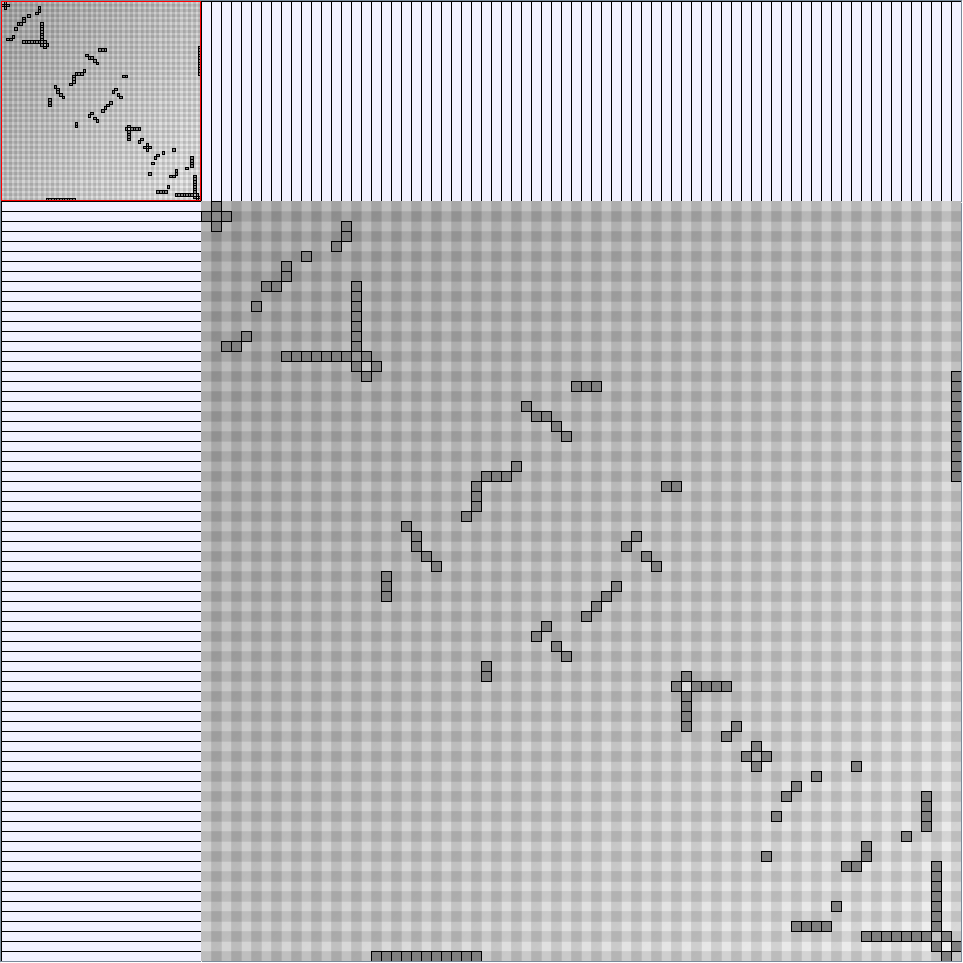
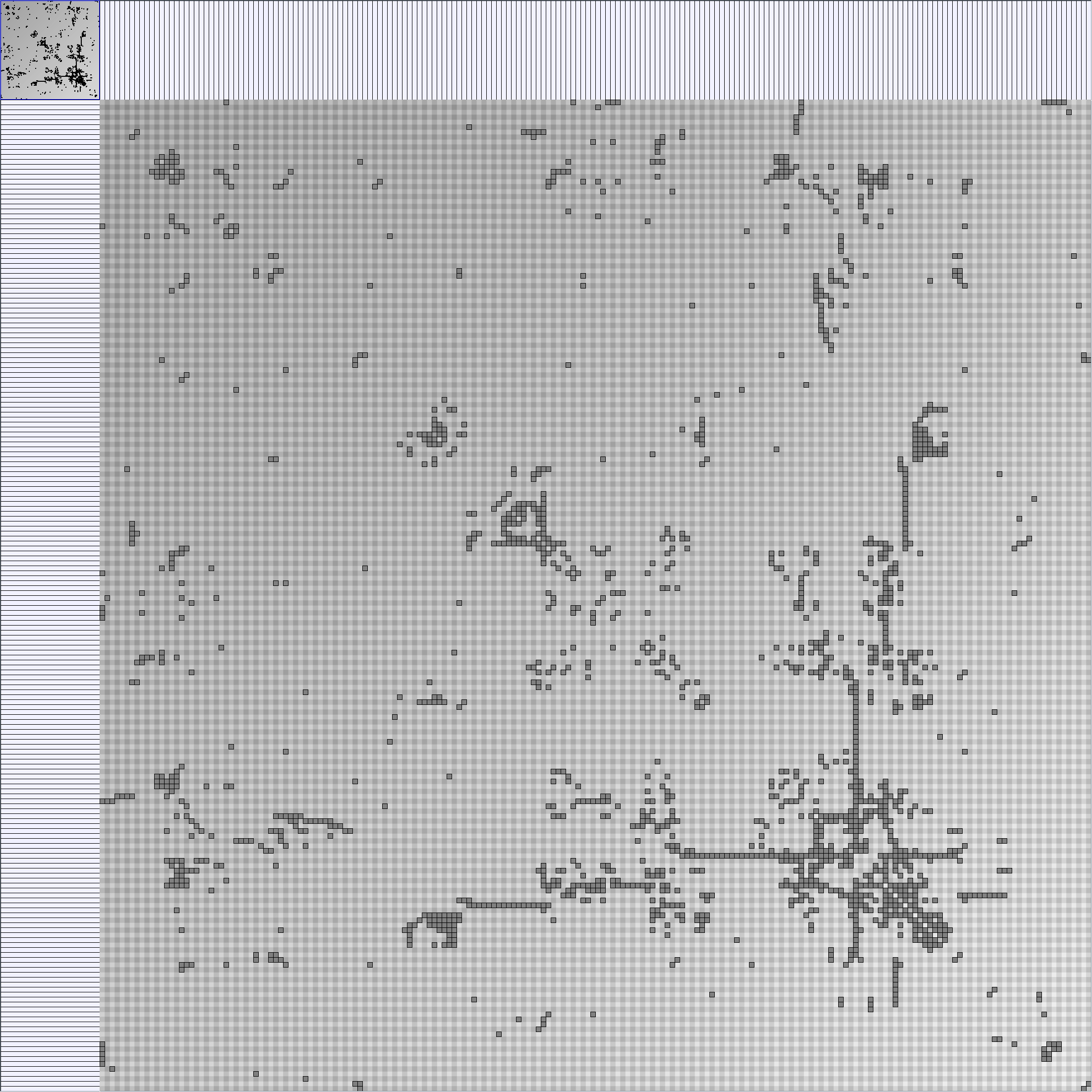
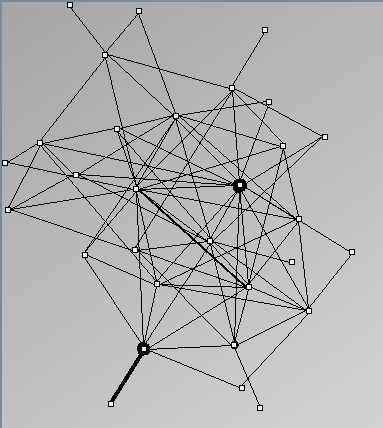
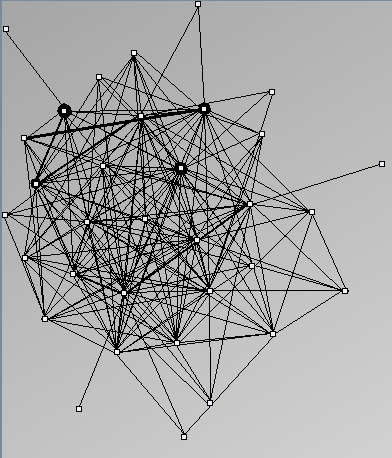
Node-Link diagrams are ordered with the linLog algorithm of Andreas Noack [Graph Drawing 2005] (with edge-repulsion coefficient of 2.5f).
Matrices are shown both with the initial order (middle image) and reordered with the TSP-Based algorithm (right image) described by Henry and Fekete [Infovis 2006].

Small-World Generators

WattsBetaSmallWorldGenerator

Parameters: numVertices (the number of nodes in the ring lattice), beta (the probability of an edge being rewired randomly; the proportion of randomly rewired edges in a graph) and degree( the number of edges connected to each vertex; the local neighborhood size). Degree must be even.

Parameters and Resulting Graph characteristics
graphs	W1	W2	W3	W4	W5	W6	W7	W8	W9	W10	W11	W12
numVertices	47	47	47	47	47	47	47	47	47	47	47	94
beta	0.1	0.3	0.5	0.7	0.9	0.3	0.3	0.3	0.3	0.7	0.1	0.1
degree	6	6	6	6	6	2	4	8	10	4	8	8
numVertices	47	47	47	47	47	47	47	47	47	47	47	94
numEdges	282	282	282	282	282	94	188	376	470	188	376	752
components	1	1	1	1	1	2	1	1	1	1	1	1
density	0.36	0.36	0.36	0.36	0.36	0.21	0.29	0.41	0.46	0.29	0.41	0.29
clusteringCoefficient	0.51	0.25	0.15	0.09	0.12	0.23	0.25	0.32	0.38	0.07	0.53	0.52
diameter	6	4	4	4	4	-	6	4	3	5	5	6
averageShortestDistance	2.97	2.4	2.32	2.3	2.29	-	3.24	2.15	1.98	2.83	2.56	3.15
minDegree	5	4	4	3	4	1	2	5	8	2	7	6
maxDegree	8	9	9	9	9	4	6	10	13	8	10	10

W1 SmallWorld_47_0.1_6.xml

W2 SmallWorld_47_0.3_6.xml

W3 SmallWorld_47_0.5_6.xml

W4 SmallWorld_47_0.7_6.xml

W5 SmallWorld_47_0.9_6.xml

W6 SmallWorld_47_0.3_2.xml

W7 SmallWorld_47_0.3_4.xml

W8 SmallWorld_47_0.3_8.xml

W9 SmallWorld_47_0.3_10.xml

W10 SmallWorld_47_0.7_4.xml

W11 SmallWorld_47_0.1_8.xml

W12 SmallWorld_94_0.1_8.xml

KleinbergSmallWorldGenerator

Parameters:latticeSize (the lattice size (length of row or column dimension)) and clusteringExponent (the clustering exponent parameter).

Parameters and Resulting Graph characteristics
graphs	W1	W2	W3	W4	W5	W6	W7	W8	W9	W10	W11
latticeSize	7	7	7	7	7	7	7	10	10	10	10
clusteringExponent	0.1	0.5	1	2	2.5	4	8	2	4	8	12
numVertices	49	49	49	49	49	49	49	100	100	100	100
numEdges	490	490	490	490	490	490	490	1000	1000	1000	1000
components	1	1	1	1	1	1	1	1	1	1	1
density	0.45	0.45	0.45	0.45	0.45	0.45	0.45	0.32	0.32	0.32	0.32
clusteringCoefficient	0.08	0.09	0.14	0.19	0.19	0.26	0.32	0.18	0.23	0.32	0.33
diameter	4	4	4	4	4	5	5	5	6	7	7
averageShortestDistance	2.38	2.36	2.37	2.44	2.48	2.54	2.73	3.1	3.57	3.65	3.68
minDegree	9	9	9	9	9	9	9	9	9	9	9
maxDegree	14	12	13	12	12	13	12	13	13	14	12

W1 SmallWorld_49_0.1.xml

W2 SmallWorld_49_0.5.xml

W3 SmallWorld_49_1.0.xml

W4 SmallWorld_49_2.0.xml

W5 SmallWorld_49_2.5.xml

W6 SmallWorld_49_4.0.xml

W7 SmallWorld_49_8.0.xml

W8 SmallWorld_100_2.0.xml

W9 SmallWorld_100_4.0.xml

W10 SmallWorld_100_8.0.xml

W11 SmallWorld_100_12.0.xml

Scale-Free Networks Generator

BarabasiAlbertGenerator

Parameters: init_vertices (number of vertices that the graph should start with), numEdgesToAttach (the number of edges that should be attached from the new vertex to pre-existing vertices at each time step) and numSteps (number of time steps). init_vertices must be superior or equal to numEdgesToAttach.

Parameters and Resulting Graph characteristics
graphs	W1	W2	W3	W4	W5	W6	W7	W8
init_vertices	4	4	4	4	2	2	2	4
numEdgesToAttach	2	2	2	1	1	1	2	4
numSteps	10	50	100	100	100	50	50	50
numVertices	14	53	104	80	76	51	52	54
numEdges	40	200	400	158	150	100	200	400
components	1	1	1	1	1	1	1	1
density	0.45	0.27	0.19	0.16	0.16	0.2	0.27	0.37
clusteringCoefficient	0.15	0.2	0.07	0.51	0.51	0.66	0.16	0.23
diameter	4	6	6	11	14	8	5	4
averageShortestDistance	2.24	2.81	3.18	5.26	5.7	3.74	2.8	2.15
minDegree	2	1	2	1	1	1	2	4
maxDegree	5	16	19	8	12	16	17	26

W1 ScaleFree_4_2_10.xml

W2 ScaleFree_4_2_50.xml

W3 ScaleFree_4_2_100.xml

W4 ScaleFree_4_1_100.xml

W5 ScaleFree_2_1_100.xml

W6 ScaleFree_2_1_50.xml

W7 ScaleFree_2_2_50.xml

W8 ScaleFree_4_4_50.xml

EppsteinPowerLawGenerator

Parameters: numVertices (the number of vertices for the generated graph), numEdges (the number of edges the generated graph will have, should be Theta(numVertices)) and r (the model parameter).

Real Social Networks

Here is a panel of undirected networks issued from scientific articles, benchmarks or contests. Social network visualization or analysis tools provide also some real datasets: Pajek [3] and UCINet [4].

Small-World

Parameters and Resulting Graph characteristics for Co-Authoring Networks	Name	Team Collaboration (with external collaborators)	Infovis component 1	Infovis component 2	Infovis component 3	Infovis component 4
Source	Collected	Contest	Contest	Contest	Contest
numNodes	146	135	48	47	32
numEdges	540	321	91	114	109
components	1	1	1	1	1
density	0.16	0.13	0.2	0.23	0.33
clusteringCoefficient	0.91	0.82	0.79	0.83	0.81
diameter	4	11	7	10	6
averageShortestDistance	2.65	4.4	3.71	3.84	2.6
minDegree	1	1	1	1	1
maxDegree	57	22	11	15	15

TeamCollaborationExternal TeamCollaborationExternal.xml

Infovis Component 1 ivComp1.xml

Infovis Component 2 ivComp2.xml

Infovis Component 3 ivComp3.xml

Infovis Component 4 ivComp4.xml

Tree-like

Parameters and Resulting Graph characteristics for Genealogy and Virus Transmission	Name	genealogy	MSTTransmission1	MSTTransmission2	HIVTransmission
Source	Pajek	Article [5]	Article[6]	Article [7]
numVertices	242	38	84	243
numEdges	510	78	182	514
components	1	1	1	1
density	0.09	0.23	0.16	0.09
clusteringCoefficient	0.66	0.53	0.52	0.65
diameter	11	10	9	23
averageShortestDistance	5.78	4.42	4.31	8.27
minDegree	1	1	1	1
maxDegree	14	7	17	20

Gondola Genealogy GondolaGen.xml

MSTTransmission 1 Mst1.xml

MSTTransmission 2 Mst2.xml

HIV Transmission Hiv.xml

Almost Complete Graphs

Parameters and Resulting Graph characteristics for Email Communication within a research lab.
Name	emailDay per person	emailWeek per person	emailMonth per person	emailYear per person	emailDay per team	emailWeek per team	emailMonth per team	emailYear per team
Source	Collected	Collected	Collected	Collected	Collected	Collected	Collected	Collected
numVertices	134	200	242	447	30	33	35	42
numEdges	442	1676	3514	11462	183	410	564	980
components	1	1	1	1	1	1	1	1
density	0.16	0.2	0.24	0.24	0.45	0.61	0.68	0.75
clusteringCoefficient	0.52	0.55	0.62	0.71	0.62	0.78	0.83	0.84
diameter	9	7	6	6	5	3	3	3
averageShortestDistance	4.29	2.92	2.52	2.42	2.17	1.71	1.57	1.45
minDegree	1	1	1	1	1	1	1	3
maxDegree	15	51	86	195	16	26	34	40