Social Network Generation: Difference between revisions
| Line 321: | Line 321: | ||
{| border="1" | {| border="1" | ||
|+ Parameters and Resulting Graph characteristics for Email Communication within | |+ Parameters and Resulting Graph characteristics for Email Communication within a research lab. | ||
|- | |- | ||
|Name||emailDay per person||emailWeek per person||emailMonth per person||emailYear per person||emailDay per team||emailWeek per team||emailMonth per team||emailYear per team | |Name||emailDay per person||emailWeek per person||emailMonth per person||emailYear per person||emailDay per team||emailWeek per team||emailMonth per team||emailYear per team | ||
Revision as of 12:39, 10 October 2006
This wiki page is still in construction...
Issues on Social Network Generation for Evaluating Visualizations
Watts and Strogatz first described in (Watts, D. J. and S. H. Strogatz (1998). "Collective dynamics of 'small-world' networks." Nature 393: 440 - 442) the concept of small-world networks. They formalized these networks as graphs with three properties: power-law degree distribution, high clustering coefficient and small average shortest path. In the same paper they propose a basic model fitting these properties consisting in a grid (fixed local neighborhood) with additional links simulating some unexpected relations support to the six degrees of separation discovered by Milgram (Milgram, S. (1967). "The small world problem." Psychology Today: 60-67). Barabási and Albert proposed an incremental model to improve it (Barabási, A.-L. and R. Albert (1999). "Emergence of Scaling in Random Networks." Science 286(5439): 509 - 512. ). Since Watts and Strogatz’ model, several have been proposed each generating networks with one or two of the described properties (power-law) but none combine the three of them.
Here are some results of available generators present in the JUNG package. Let's note that for each network generated we only keep the biggest component. Generators present in Pajek[1] and Geomi[2] are incremental scale-free networks generators such as the Barabasi and Albert model.
Small-World Generators
WattsBetaSmallWorldGenerator
Parameters: numVertices (the number of nodes in the ring lattice), beta (the probability of an edge being rewired randomly; the proportion of randomly rewired edges in a graph) and degree( the number of edges connected to each vertex; the local neighborhood size). Degree must be even.
| graphs | W1 | W2 | W3 | W4 | W5 | W6 | W7 | W8 | W9 | W10 | W11 | W12 |
| numVertices | 47 | 47 | 47 | 47 | 47 | 47 | 47 | 47 | 47 | 47 | 47 | 94 |
| beta | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 | 0.3 | 0.3 | 0.3 | 0.3 | 0.7 | 0.1 | 0.1 |
| degree | 6 | 6 | 6 | 6 | 6 | 2 | 4 | 8 | 10 | 4 | 8 | 8 |
| numVertices | 47 | 47 | 47 | 47 | 47 | 47 | 47 | 47 | 47 | 47 | 47 | 94 |
| numEdges | 282 | 282 | 282 | 282 | 282 | 94 | 188 | 376 | 470 | 188 | 376 | 752 |
| components | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 |
| density | 0.36 | 0.36 | 0.36 | 0.36 | 0.36 | 0.21 | 0.29 | 0.41 | 0.46 | 0.29 | 0.41 | 0.29 |
| clusteringCoefficient | 0.51 | 0.25 | 0.15 | 0.09 | 0.12 | 0.23 | 0.25 | 0.32 | 0.38 | 0.07 | 0.53 | 0.52 |
| diameter | 6 | 4 | 4 | 4 | 4 | - | 6 | 4 | 3 | 5 | 5 | 6 |
| averageShortestDistance | 2.97 | 2.4 | 2.32 | 2.3 | 2.29 | - | 3.24 | 2.15 | 1.98 | 2.83 | 2.56 | 3.15 |
| minDegree | 5 | 4 | 4 | 3 | 4 | 1 | 2 | 5 | 8 | 2 | 7 | 6 |
| maxDegree | 8 | 9 | 9 | 9 | 9 | 4 | 6 | 10 | 13 | 8 | 10 | 10 |
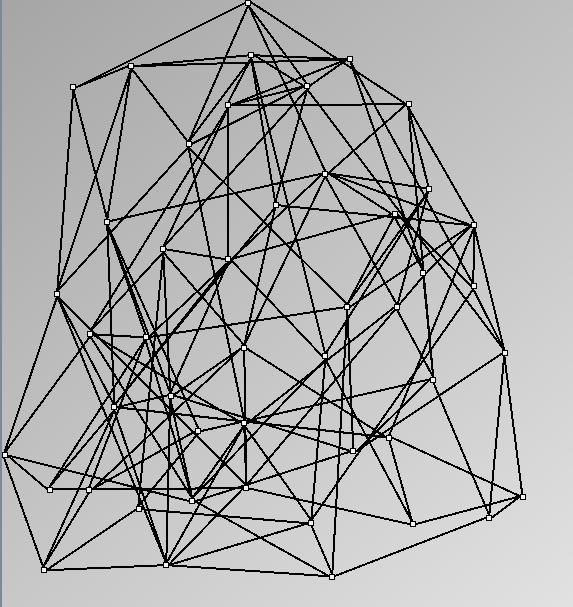
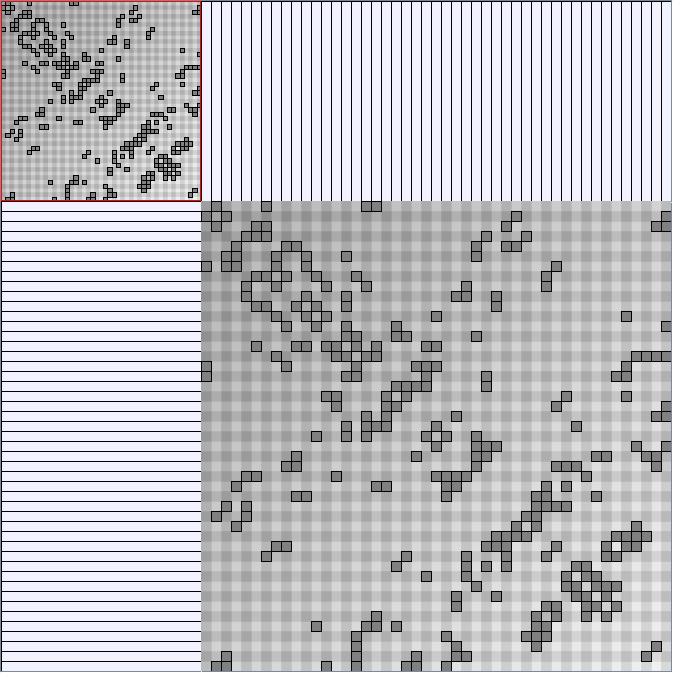
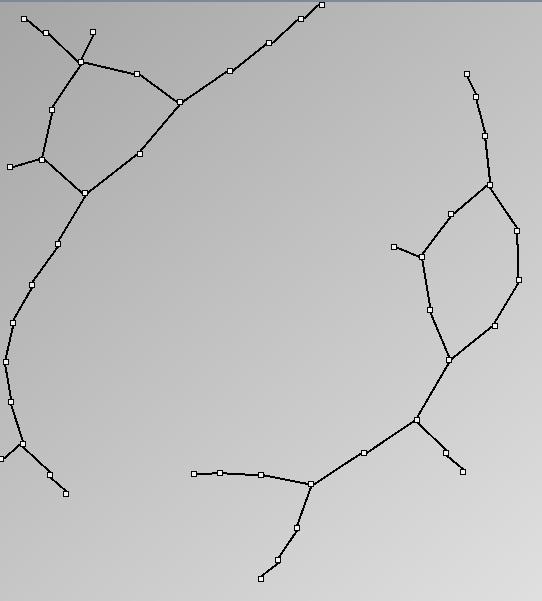
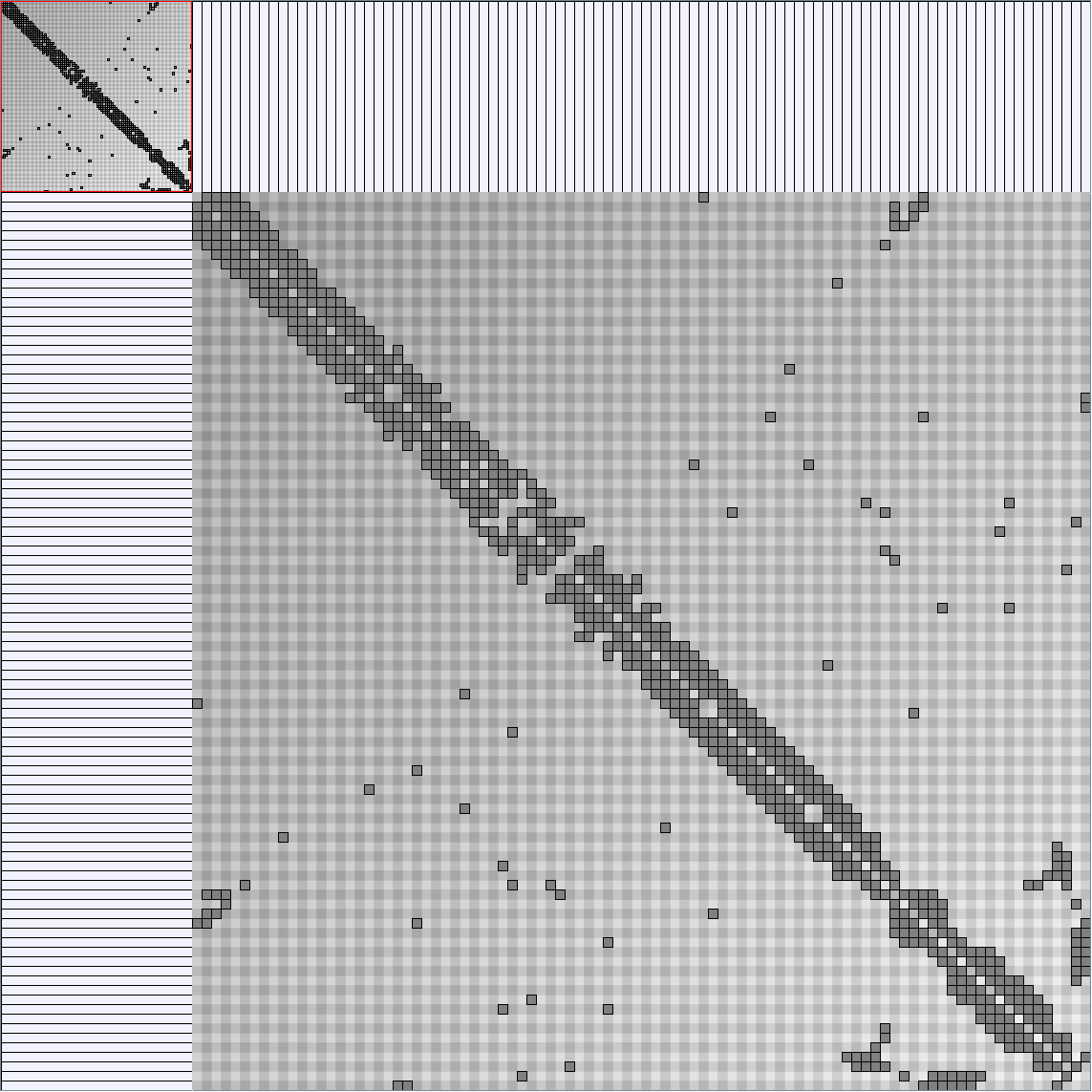
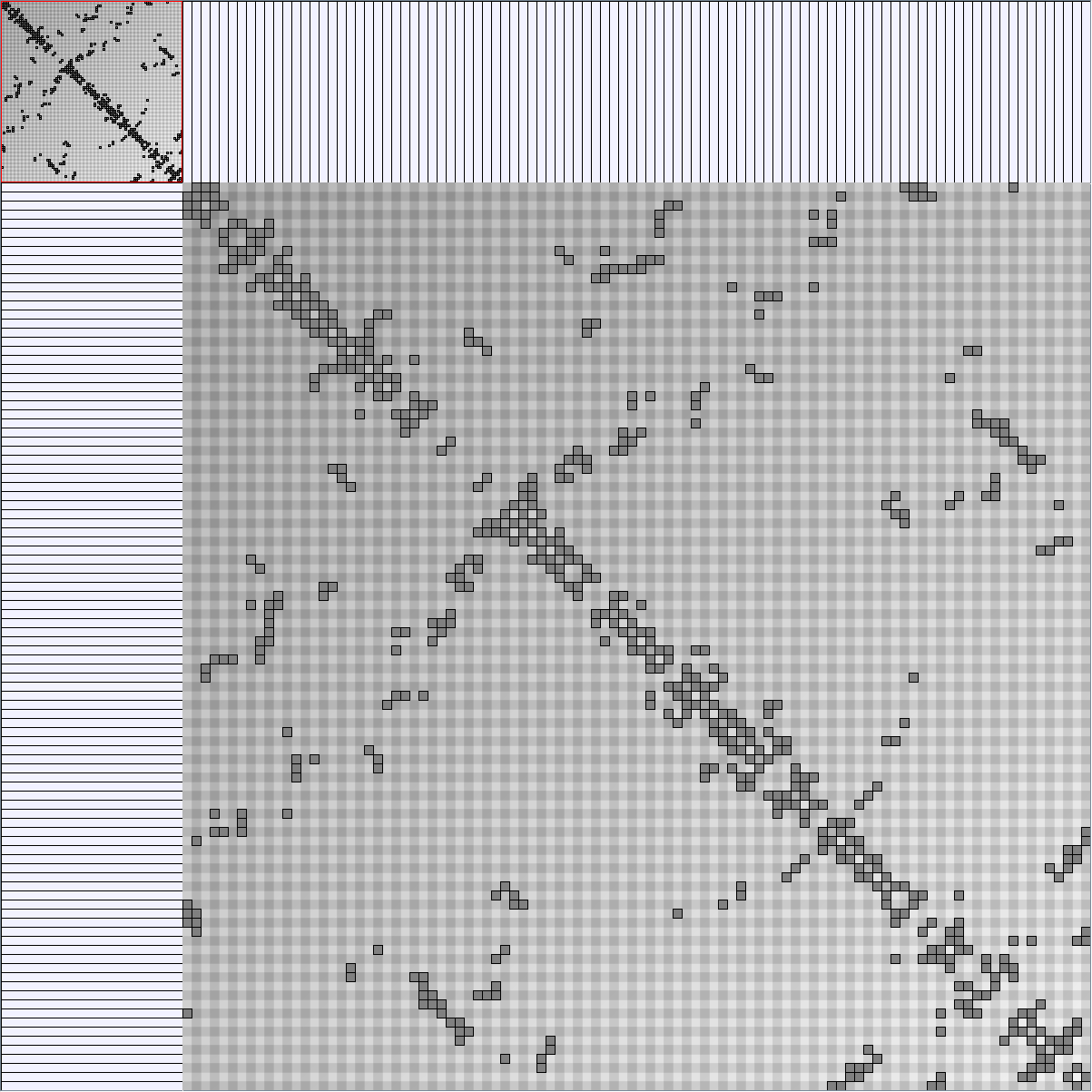
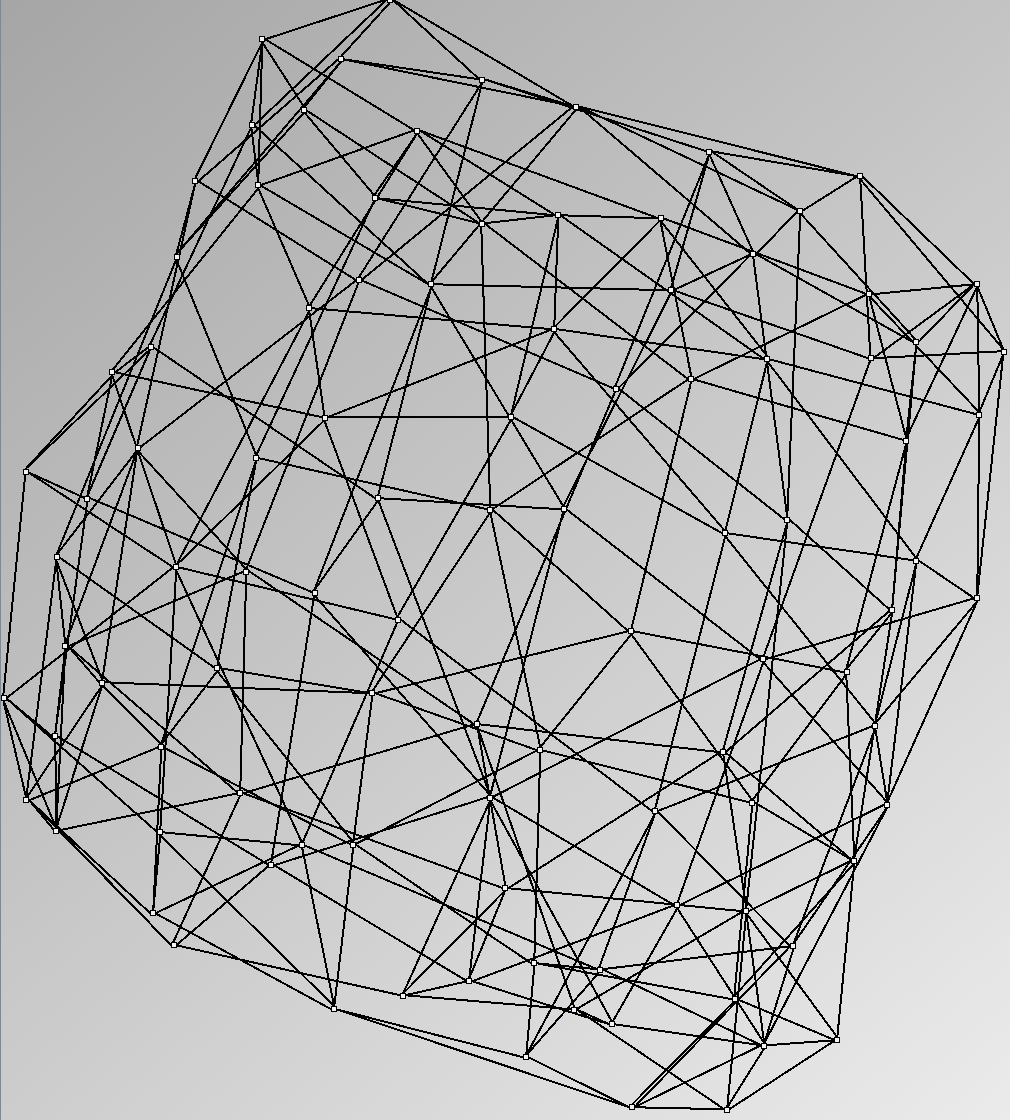
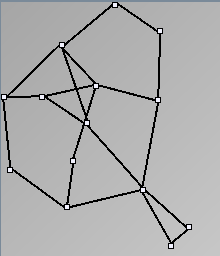
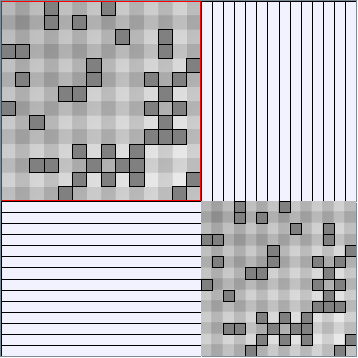
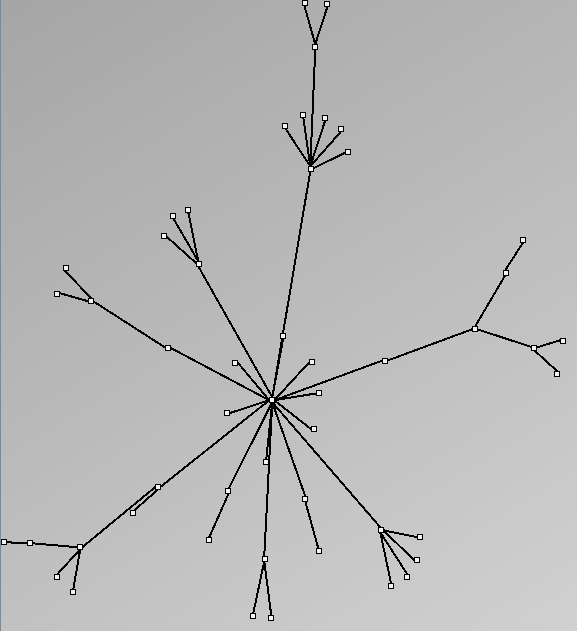
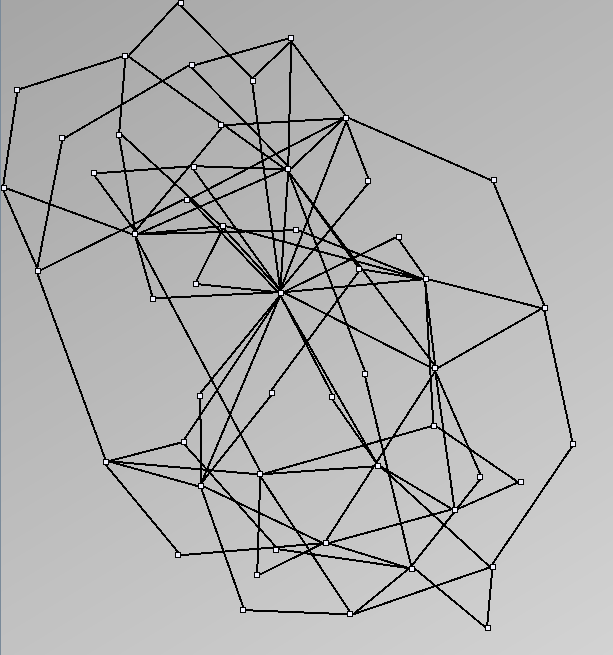
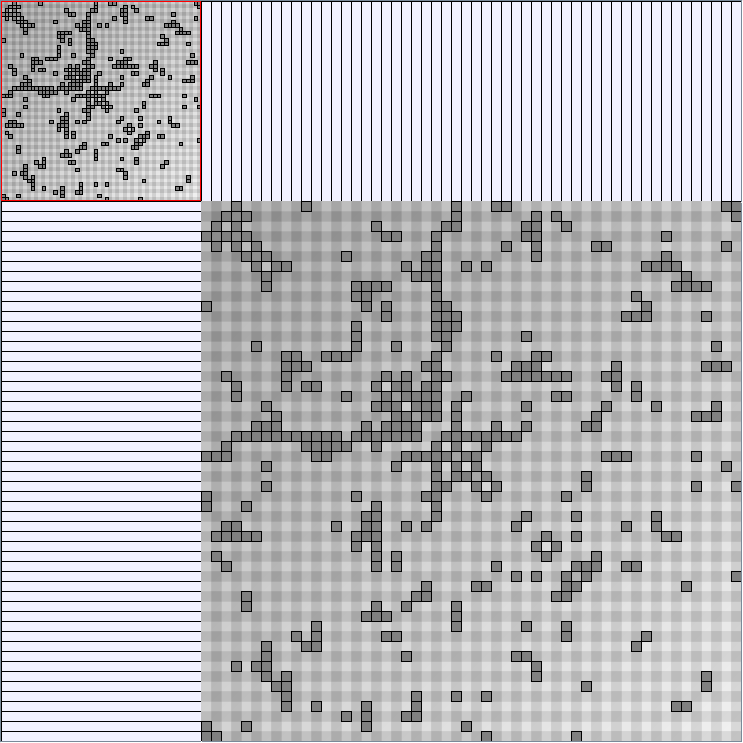
GraphMl files and Pictures:
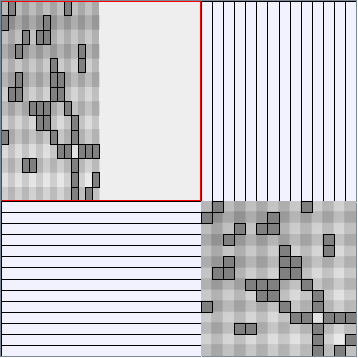
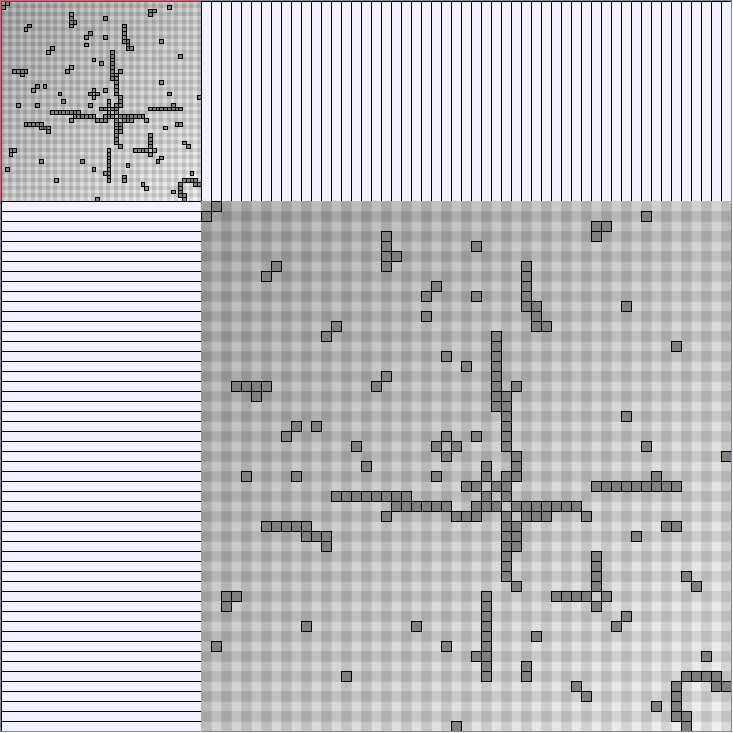
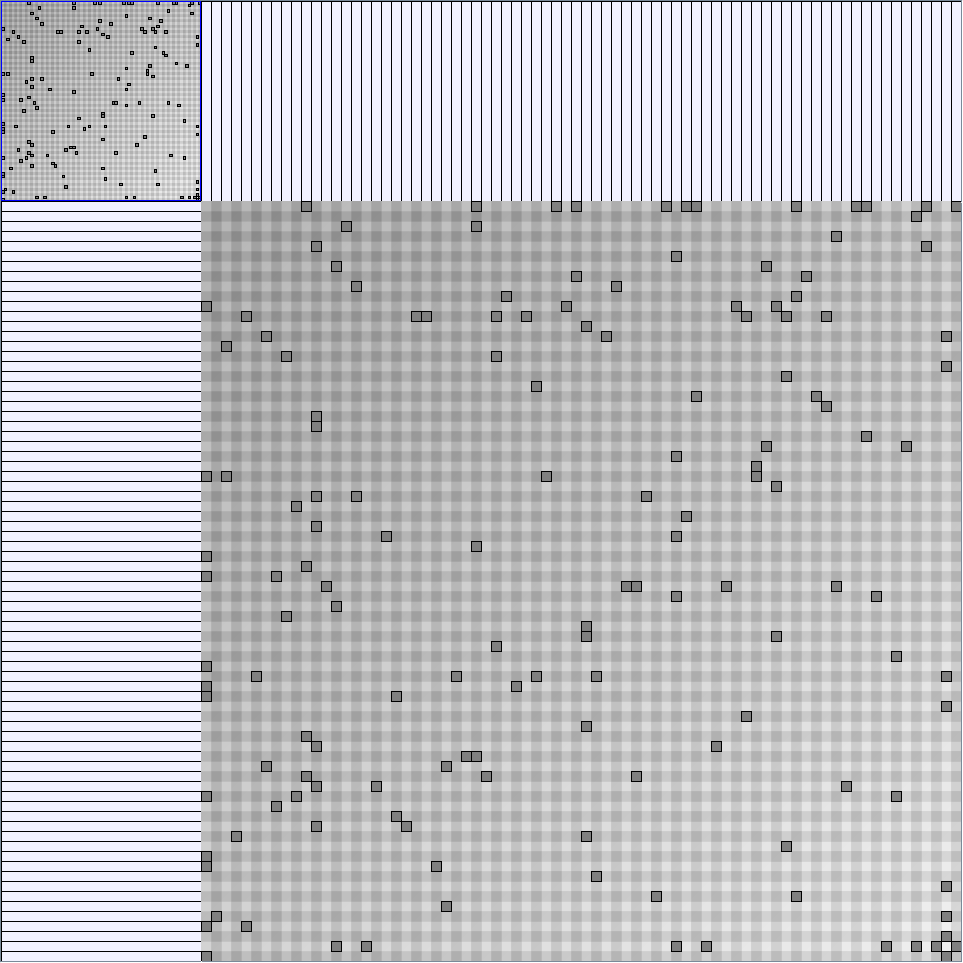
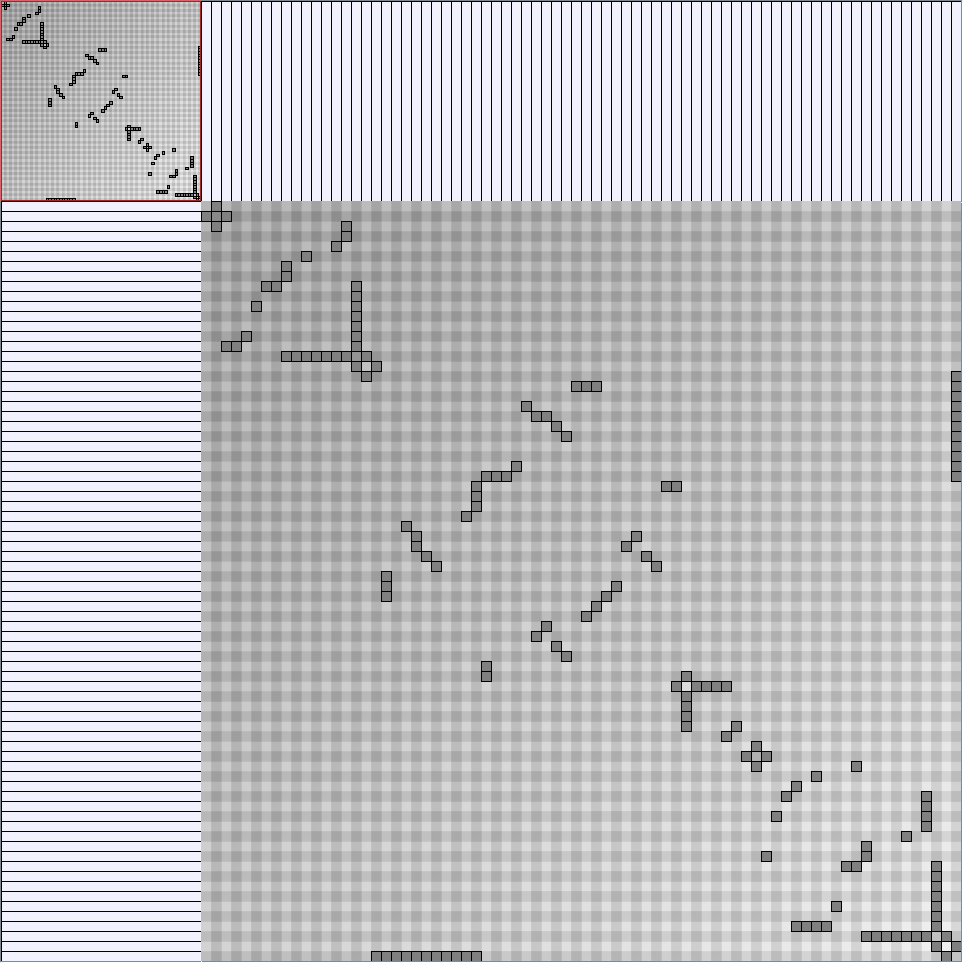
- Node-Link diagrams are ordered with the linLog algorithm of Andreas Noack [Graph Drawing 2005] (with edge-repulsion coefficient of 2.5f).
- Matrices are shown both with the initial order (middle image) and reordered with the TSP-Based algorithm (right image) described by Henry and Fekete [Infovis 2006].
W2 SmallWorld_47_0.3_6
W3 SmallWorld_47_0.5_6
W4 SmallWorld_47_0.7_6
W5 SmallWorld_47_0.9_6
W6 SmallWorld_47_0.3_2
W7 SmallWorld_47_0.3_4
W8 SmallWorld_47_0.3_8
W9 SmallWorld_47_0.3_10
W10 SmallWorld_47_0.7_4
W11 SmallWorld_47_0.1_8
W12 SmallWorld_94_0.1_8
KleinbergSmallWorldGenerator
Parameters:latticeSize (the lattice size (length of row or column dimension)) and clusteringExponent (the clustering exponent parameter).
| graphs | W1 | W2 | W3 | W4 | W5 | W6 | W7 | W8 | W9 | W10 | W11 |
| latticeSize | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 10 | 10 | 10 | 10 |
| clusteringExponent | 0.1 | 0.5 | 1 | 2 | 2.5 | 4 | 8 | 2 | 4 | 8 | 12 |
| numVertices | 49 | 49 | 49 | 49 | 49 | 49 | 49 | 100 | 100 | 100 | 100 |
| numEdges | 490 | 490 | 490 | 490 | 490 | 490 | 490 | 1000 | 1000 | 1000 | 1000 |
| components | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| density | 0.45 | 0.45 | 0.45 | 0.45 | 0.45 | 0.45 | 0.45 | 0.32 | 0.32 | 0.32 | 0.32 |
| clusteringCoefficient | 0.08 | 0.09 | 0.14 | 0.19 | 0.19 | 0.26 | 0.32 | 0.18 | 0.23 | 0.32 | 0.33 |
| diameter | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 6 | 7 | 7 |
| averageShortestDistance | 2.38 | 2.36 | 2.37 | 2.44 | 2.48 | 2.54 | 2.73 | 3.1 | 3.57 | 3.65 | 3.68 |
| minDegree | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| maxDegree | 14 | 12 | 13 | 12 | 12 | 13 | 12 | 13 | 13 | 14 | 12 |
W1 SmallWorld_49_0.1
W2 SmallWorld_49_0.5
W3 SmallWorld_49_1.0
W4 SmallWorld_49_2.0
W5 SmallWorld_49_2.5
W6 SmallWorld_49_4.0
W7 SmallWorld_49_8.0
W8 SmallWorld_100_2.0
W9 SmallWorld_100_4.0
W10 SmallWorld_100_8.0
W11 SmallWorld_100_12.0
Scale-Free Networks Generator
BarabasiAlbertGenerator
Parameters: init_vertices (number of vertices that the graph should start with), numEdgesToAttach (the number of edges that should be attached from the new vertex to pre-existing vertices at each time step) and numSteps (number of time steps). init_vertices must be superior or equal to numEdgesToAttach.
| graphs | W1 | W2 | W3 | W4 | W5 | W6 | W7 | W8 |
| init_vertices | 4 | 4 | 4 | 4 | 2 | 2 | 2 | 4 |
| numEdgesToAttach | 2 | 2 | 2 | 1 | 1 | 1 | 2 | 4 |
| numSteps | 10 | 50 | 100 | 100 | 100 | 50 | 50 | 50 |
| numVertices | 14 | 53 | 104 | 80 | 76 | 51 | 52 | 54 |
| numEdges | 40 | 200 | 400 | 158 | 150 | 100 | 200 | 400 |
| components | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| density | 0.45 | 0.27 | 0.19 | 0.16 | 0.16 | 0.2 | 0.27 | 0.37 |
| clusteringCoefficient | 0.15 | 0.2 | 0.07 | 0.51 | 0.51 | 0.66 | 0.16 | 0.23 |
| diameter | 4 | 6 | 6 | 11 | 14 | 8 | 5 | 4 |
| averageShortestDistance | 2.24 | 2.81 | 3.18 | 5.26 | 5.7 | 3.74 | 2.8 | 2.15 |
| minDegree | 2 | 1 | 2 | 1 | 1 | 1 | 2 | 4 |
| maxDegree | 5 | 16 | 19 | 8 | 12 | 16 | 17 | 26 |
W1 ScaleFree_4_2_10
W2 ScaleFree_4_2_50
W3 ScaleFree_4_2_100
W4 ScaleFree_4_1_100
W5 ScaleFree_2_1_100
W6 ScaleFree_2_1_50
W7 ScaleFree_2_2_50
W8 ScaleFree_4_4_50
EppsteinPowerLawGenerator
Parameters: numVertices (the number of vertices for the generated graph), numEdges (the number of edges the generated graph will have, should be Theta(numVertices)) and r (the model parameter).
Issues on using real Social Networks for Evaluating Visualizations
Here is a panel of undirected networks issued from scientific articles, benchmarks or contests. Social network visualization or analysis tools provide also some real datasets: Pajek [3] and UCINet [4].
| Name | emailDay per person | emailWeek per person | emailMonth per person | emailYear per person | emailDay per team | emailWeek per team | emailMonth per team | emailYear per team |
| Source | Collected | Collected | Collected | Collected | Collected | Collected | Collected | Collected |
| numVertices | 134 | 200 | 242 | 447 | 30 | 33 | 35 | 42 |
| numEdges | 442 | 1676 | 3514 | 11462 | 183 | 410 | 564 | 980 |
| components | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| density | 0.16 | 0.2 | 0.24 | 0.24 | 0.45 | 0.61 | 0.68 | 0.75 |
| clusteringCoefficient | 0.52 | 0.55 | 0.62 | 0.71 | 0.62 | 0.78 | 0.83 | 0.84 |
| diameter | 9 | 7 | 6 | 6 | 5 | 3 | 3 | 3 |
| averageShortestDistance | 4.29 | 2.92 | 2.52 | 2.42 | 2.17 | 1.71 | 1.57 | 1.45 |
| minDegree | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 3 |
| maxDegree | 15 | 51 | 86 | 195 | 16 | 26 | 34 | 40 |
| Name | Team Collaboration (with external collaborators) | Team Collaboration (within the team) | Infovis component 1 | Infovis component 2 | Infovis component 3 | Infovis component 4 |
| Source | Collected | Collected | Contest | Contest | Contest | Contest |
| numNodes | 146 | 96 | 135 | 48 | 47 | 32 |
| numEdges | 540 | 316 | 321 | 91 | 114 | 109 |
| components | 1 | 1 | 1 | 1 | 1 | 1 |
| density | 0.16 | 0.19 | 0.13 | 0.2 | 0.23 | 0.33 |
| clusteringCoefficient | 0.91 | 0.91 | 0.82 | 0.79 | 0.83 | 0.81 |
| diameter | 4 | 5 | 11 | 7 | 10 | 6 |
| averageShortestDistance | 2.65 | 2.81 | 4.4 | 3.71 | 3.84 | 2.6 |
| minDegree | 1 | 1 | 1 | 1 | 1 | 1 |
| maxDegree | 57 | 29 | 22 | 11 | 15 | 15 |