Circle Packing

Authors

• Hongan Wang
  
• Guozhong Dai
  
• Weixin Wang
  
• Hui Wang
  

Short description

Circle packing is a method to visualize large hierarchical data using nested circles. Inspired by treemaps and Grokker, Wang et al. developed a layout algorithm for tree structures which gives a good overview for large data sets. Tangent circles represent the brother nodes at the same level. The different leves are shown by nested circles (2D) or nested cylinders (3D). An advantage of this algorithm is the good overview for large data sets and it is easy to make out groupings and structural relationships.

[Wang, W. et al., 2006]

Figures

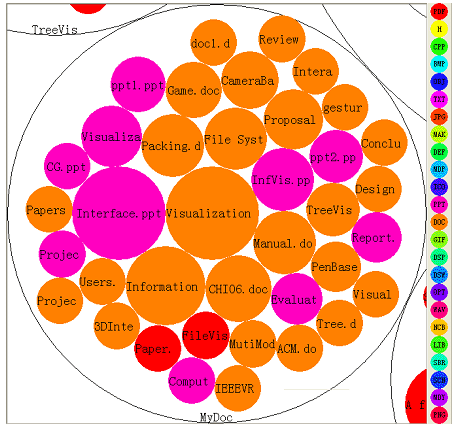
The tree nodes at different levels are represented by nested circles. Brother nodes are packed into the root node. If a node has children they are packed into it.

Packing circles with random radii. The shape is basically convex.

3D nested cylinders and spheres

Userinterface: directories are represented by white circles.
The Color of the inner circles shows the filetype and the file sizes determine the radii.

Suitable Datatypes

Suitable Datatypes for this visualization technique are (large) hierarchical data structures.

Important Citations

The visualization of hierarchical information structures is an important topic in the visualization community. Most of the work concentrated on the challenge to display large hierarchies in a comprehensible form.

[Wang, W. et al., 2006]

The circles of different radii are suitable for representing large numbers of brother nodes. There is no overlapping between any two circles, which ensures each circle is visible. The circles are to be packed as close as possible to save display space. A new circle is always placed outside the front-chain and beside the circle whose center is nearest to the origin, which ensures that the shape of front-chain is basically convex like a circle.

[Wang, W. et al., 2006]

The layout algorithm for tree visualization leads to a simultaneously clearer and more compact visualization of a hierarchy than rectangular views and node-link diagrams. The visualization has the advantage over retangular layouts of allowing even very small nodes to remain visible without contorted aspect ratios. Though the use of display space is not more efficient than rectangular layouts, the space is helpful to see structural relationships and is easy to select (click) a node.

[Wang, W. et al., 2006]

Evaluation

Twenty-one students tested the file visualization tool for two weeks. Their feedback gave a 67 percent positive rating, a 22 percent neutral rating and a 11 percent negative rating.

Mentioned advantages:

• robust and efficient for thousands of files
• friendly interface which is easy to use
• interface needs less operation than traditional files management systems to find a file
• user interface has a high efficiency
• clear bird view of the whole files
• quickly zoom in/out

Mentioned disadvantages:

• difficult to display a long file name fully
• no file names shown in 3D view
• difficult to do copy/paste-operations

Internal Links

• Treemap

External Links

[grokker] Grokker

References

[Wang, W. et al. 2006] Wang et al. Visualization of large hierarchical data by circle packing. In Proceedings of the SIGCHI conference on Human Factors in computing systems, pages 517-520, Montréal, Québec, Canada, 2006: ACM Press.

Evaluation Reference

[Wang, W. et al. 2006] Wang et al. Visualization of large hierarchical data by circle packing. In Proceedings of the SIGCHI conference on Human Factors in computing systems, pages 517-520, Montréal, Québec, Canada, 2006: ACM Press.