Circle Packing: Difference between revisions
| (5 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
== Short description == | == Short description == | ||
Circle packing is a method to visualize large | Circle packing is a method to visualize large amounts of hierarchically structured data. Inspired by [[Treemap|treemaps]] and [http://www.grokker.com Grokker], Wang et al. developed this layout algorithm for tree structures: Tangent circles represent brother nodes at the same level; to visualize the hierarchy, all children of a node are packed into that node (and thus determine its size). The size of a leaf-node can represent an arbitrary property, such as file size. An advantage of this algorithm is the good overview of large data sets and the clear representation of groupings and structural relationships. | ||
As a space-filling technique, Circle Packing visualizes information as spatial extension. The algorithm on which it is based is related to the mathematical problem with the same name ([http://en.wikipedia.org/wiki/Sphere_packing#Circle_packing Wikipedia article]). It places any number of brother nodes, represented by circles, in an arrangement that has a high density and retains a convex shape approximating a circle as the amount of nodes grows. Due to this property, a set of brother nodes can always be packed into its (also circle-shaped) parent node. | |||
Compared to that of [[Treemap|treemaps]], a visualization generated by this technique is - while possibly a bit less space-efficient - easier to comprehend visually while it retains the ability to (theoretically) display all hierarchies at once. This, of course, requires an apt user interface to easily zoom into the structure if that is required to see the leaf nodes in detail. | |||
The authors have also demonstrated an extension of the visualization into the third dimension by using cylinders with a height value representing the level of a node. | |||
== Figures == | == Figures == | ||
| Line 42: | Line 46: | ||
Suitable Datatypes for this visualization technique are (large) hierarchical data structures. | Suitable Datatypes for this visualization technique are (large) hierarchical data structures. | ||
== Important Citations == | == Important Citations == | ||
Latest revision as of 15:27, 25 April 2007
Authors
- Hongan Wang
- Guozhong Dai
- Weixin Wang
- Hui Wang
Short description
Circle packing is a method to visualize large amounts of hierarchically structured data. Inspired by treemaps and Grokker, Wang et al. developed this layout algorithm for tree structures: Tangent circles represent brother nodes at the same level; to visualize the hierarchy, all children of a node are packed into that node (and thus determine its size). The size of a leaf-node can represent an arbitrary property, such as file size. An advantage of this algorithm is the good overview of large data sets and the clear representation of groupings and structural relationships.
As a space-filling technique, Circle Packing visualizes information as spatial extension. The algorithm on which it is based is related to the mathematical problem with the same name (Wikipedia article). It places any number of brother nodes, represented by circles, in an arrangement that has a high density and retains a convex shape approximating a circle as the amount of nodes grows. Due to this property, a set of brother nodes can always be packed into its (also circle-shaped) parent node.
Compared to that of treemaps, a visualization generated by this technique is - while possibly a bit less space-efficient - easier to comprehend visually while it retains the ability to (theoretically) display all hierarchies at once. This, of course, requires an apt user interface to easily zoom into the structure if that is required to see the leaf nodes in detail.
The authors have also demonstrated an extension of the visualization into the third dimension by using cylinders with a height value representing the level of a node.
Figures
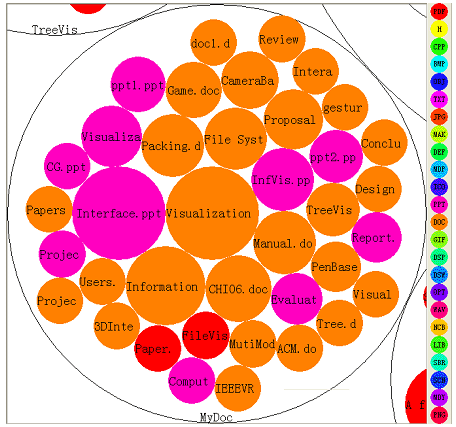
The tree nodes at different levels are represented by nested circles. Brother nodes are packed into the root node. If a node has children they are packed into it.
Packing circles with random radii. The shape is basically convex.
3D nested cylinders and spheres
Userinterface: directories are represented by white circles.
The Color of the inner circles shows the filetype and the file sizes determine the radii.
Suitable Datatypes
Suitable Datatypes for this visualization technique are (large) hierarchical data structures.
Important Citations
Evaluation
Twenty-one students tested the file visualization tool for two weeks. Their feedback was a 67 percent positive rating, a 22 percent neutral rating and a 11 percent negative rating.
Mentioned advantages:
- robust and efficient for thousands of files
- friendly interface which is easy to use
- interface needs less operation than traditional files management systems to find a file
- user interface has a high efficiency
- clear bird view of the whole files
- quickly zoom in/out
Mentioned disadvantages:
- difficult to display a long file name fully
- no file names shown in 3D view
- difficult to do copy/paste-operations
Internal Links
External Links
[grokker] Grokker
References
[Wang, W. et al. 2006] Wang et al. Visualization of large hierarchical data by circle packing. In Proceedings of the SIGCHI conference on Human Factors in computing systems, pages 517-520, Montréal, Québec, Canada, 2006: ACM Press.
Evaluation Reference
[Wang, W. et al. 2006] Wang et al. Visualization of large hierarchical data by circle packing. In Proceedings of the SIGCHI conference on Human Factors in computing systems, pages 517-520, Montréal, Québec, Canada, 2006: ACM Press.